このように「○のつくことば遊び」「しりとり」「手遊び」「ことば階段」などのゲーム性をもった活動をどんどんおこなっていきます。このような友だちとのやり取りをとおして、社会のルールも自然に学んでいくことができます。

社会のルールも自然に学んでいくことができる（画像はイメージです／PIXTA）

「数の概念」を理解してもらう必要がある

数の学習は日常生活の周りにおこる事象を合理的にとらえていくためのものであるといわれます。思考は合理性が増すにしたがい、抽象的な概念にまとめられてきます。数字は「1、2、3、4、5、6、7、8、9、10」と物事を個別化し、一定の秩序をもって考えていくための手段として、具体的な事象を抽象的な概念にまとめたものと考えることができます。

たとえば、数の概念を身につけることによって、家族の人数とケーキがきちんと一人ずつにいきわたって食べることができるとか、A道よりB道を通った方が駅に近いとか、AよりBの方が大きくて自分には得になるなどと物事を合理的に考えるようになることだと思います。それが、算数を学ぶ喜びの一つかもしれません。

また、抽象性という点では、大きな象を数えても「1、2」という数字になります。小さな蟻を数えてもやはり、同じ「1、2」の数字に置き換えることができます。さらに、この数の概念は猫を「1、2、3」と数えても、「3番目の猫」と「3匹の猫」という概念の二面性をもっています。

数には、物事を考えるときの汎用性があります。数には順序数、集合数という2つの概念の側面があります（図表1）。

［図表1］数概念の二面性

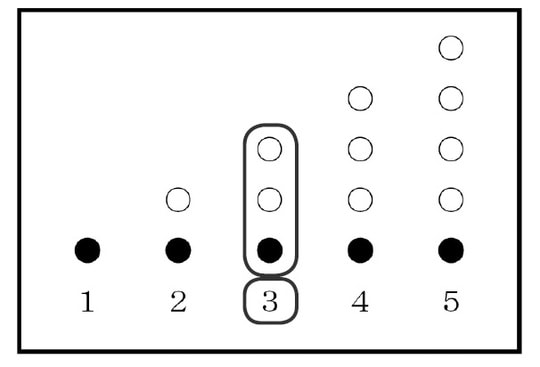
図表1の黒丸は順序数としての数です。白丸は、まとまりとしての集合数です。数を量と
して覚えていくためには、集合数としての数概念を覚えていく必要があります。

図表2は数概念を図式化したものです。数概念は、「具体物」と「数詞」と「数字」の３つの関係が結びつく必要があります。

［図表2］数概念の関係

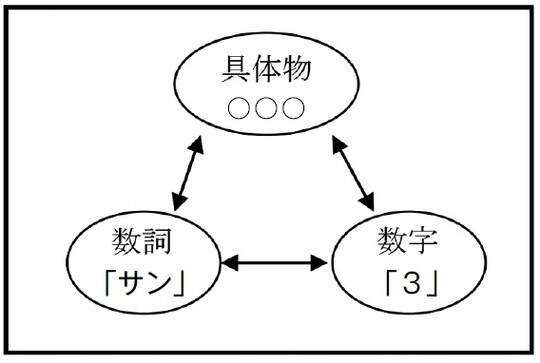
たし算、ひき算をマスターするためには…

たとえば、具体物が3つ並んでいるのを見て、「サン」（数詞）と「3」（数字）が、相互に結びつかないと、たし算、ひき算はできるようになりません。