損失を忌避しながらも「結果的に損する選択」をとる謎
本連載でここまでお話ししてきて、結局、私たちが生命保険に加入しつつ、宝くじを買ってしまう理由を疑問に思う人がいるかもしれません。
「利得の局面ではリスクを回避して、損失の局面であればリスク*を追求する」というのがプロスペクト理論で説明される、ヒトが持つリスクの状況下での基本方針でした(*経済学では一般的に、ある出来事が起こりえるときの不確実さのことを「リスク」と呼びます。悪いことでも良いことでも、起こりえる出来事が不確実であれば、なんでもリスクです)。
しかし、宝くじは、当たると大きな賞金がもらえるリスクの高いギャンブルです。つまり、“儲け”が期待できる状況でも、多くの人はリスクを平然と受け入れていることになってしまいます。なぜ、このようになってしまうのでしょうか。
そこで、行動経済学者・カーネマン氏とトヴェルスキー氏は考えました。
「リスクのある状況下で、ヒトが物事の価値を“現状からの変化”で主観的に捉えているのなら、確率についても主観的に捉えているのではないか?」
そこで示されるのが、これからご紹介する「確率加重関数」です。
0%でなければ、低確率でも“意外とありそう”に感じる
主張はいたってシンプルです。
61%と63%。差は大きいと思いますか? たったの2%の差に過ぎません。
では、98%と100%だったらどうでしょう。同じく2%の差ですから、やはり大差ないと思えるでしょうか?
おそらく多数の人は、100%かどうかを大きな違いと捉えるはずです。
しかし、そうなると数値上は同じ0.02の違いなのに、98%と100%との間は“もっと大きな違いがある”と感じていることになります。
こうした状況をカーネマン氏たちは、「何か出来事が起こる客観的な確率を、ヒトの頭で評価した主観的な確率(心理的な確率)が、どこかのタイミングで重く評価しているはずなのではないか」と説明します(図表1)。
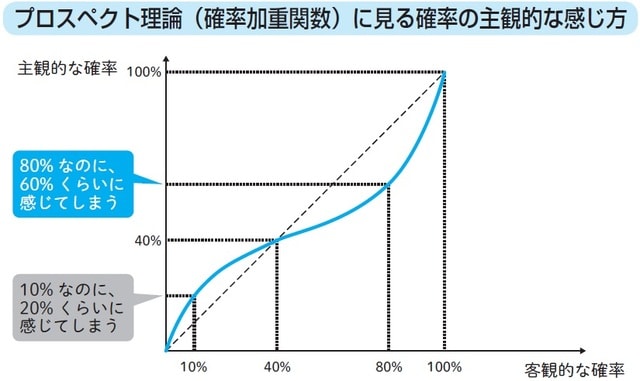
みんなが100%を大きく評価したように、実験で見られたひとつの傾向は、より確実な確率を重く受け止め評価していたので、これを「確実性効果」と言います。結果、少しでも確実ではなくなると、その主観的な評価も大きく下がります。
実験でのもうひとつの傾向は、「非常に低い確率事象も重く受け止めてしまう」ということです。たとえば、年末ジャンボの当せん確率0.000005%と0.00001%。いちいち0の数を数えてないですよね。
全くありえないこと、つまり0%ではないと思ってしまうと、いきなり「意外とありえそうな出来事」のように扱ってしまっているわけです。これは「可能性効果」と呼ばれます。





























