検索
「同様に確からしい」ことを確かめる
また、天気には概（おおむ）ね〈晴れ・曇り・雨・雪〉の4種類がありますが、毎日「明日、雪になる確率は1/4だ」と考えるのも同様の理由から誤りです。
ジャンボ宝くじの場合、1等は2000万枚の中に1枚含まれています。今、目の前に1等を含む2000万枚の宝くじがあるとして、その中から1枚選んで引くことをイメージしてください。
当然、2000万通りの選び方があるわけですが、どの1枚を引くことも「同じ程度に期待」できます。2000万通りの引き方はどれも同様に確からしいので、1等が当たる確率を2000万分の1と考えるのは妥当です。
2枚のコインの話に戻しましょう。
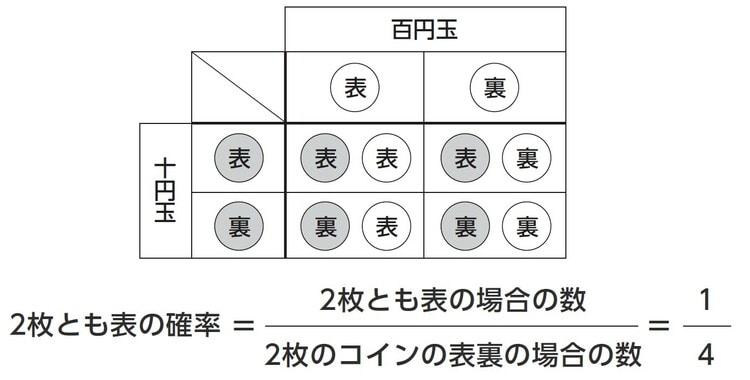
2枚のコインが十円玉と百円玉の場合を考えてみればわかるように、2枚のコインのうち一方が表で他方が裏であるケースには、十円玉が表で百円玉が裏になるケースと十円玉が裏で百円玉が表になるケースがあります。
すなわち、（十円玉が表・百円玉が裏）と（十円玉が裏・百円玉が表）をまとめて（表・裏）として1通りに考えてしまうと、この（表・裏）は（表・表）や（裏・裏）と同様に確からしくなくなるため、誤りなのです（［図表2］）。
［図表2］同様に確からしいものの数の数え方
永野 裕之
永野数学塾
塾長
《最新のDX動向・人気記事・セミナー情報をお届け！》
≫≫≫DXナビ メルマガ登録はこちら
