「ゲーム理論」は、ハンガリー出身のアメリカの数学者、ジョン・フォン＝ノイマンによって示され、アメリカ人の数学者でノーベル経済学賞を受賞したジョン・ナッシュによって発展しました。現在では、経済学の多くの分野で採用されており、欠かせないツールとなっています。

 

ナッシュ均衡

◆相談できない2人のゲーム

まずは囚人のジレンマというゲームを見てみましょう。ゲームに登場する2人をプレイヤーと呼びましょう。各プレイヤーはいくつかの選択肢＝戦略を持っており、「各プレイヤーは、自己の利得が最大になるような戦略を選択する」というルールに基づいて行動します。利得とはゲームの得点のことで、利得表という表で得点が事前に示されています。

 

 

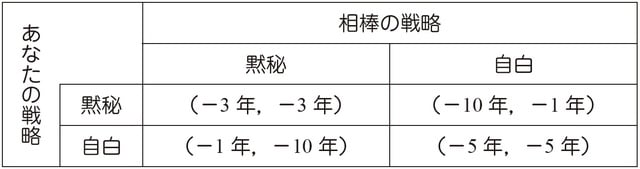
看守が2人に見せたのは次ページの利得表です。2人のプレイヤーは「黙秘」と「自白」の2つの戦略が与えられています。

 

図表1の数字は（あなたの利得、相棒の利得）を表しています。刑に服するのはマイナスのことであるため、懲役3年を－3年という形で表現しています。

 

 

あなたが自白して相棒が黙秘すると、利得は左下の（－1年、－10年）になり、あなたは懲役1年、相棒は懲役10年となります。互いに相談できないため、相手が何を選択するのか分かりません。このような状況でどのように考えたらいいでしょうか？

 

◆ゲームを解く

相棒が何を選択するのか分からないので、黙秘と自白の両方のパターンを考えましょう。

 

まずは、相棒が黙秘を選んだ場合、つまり、利得表の左半分を考えます（右半分は隠しておきましょう）。あなたが黙秘をすると利得は－3、自白をすると利得は－1となります。この場合、－1を選んだ方が利得が大きくなります。あなたの戦略ということで、左下のあなたの利得の下に○を付けておきましょう。

 

次に、相棒が自白を選んだ場合、利得表の右半分です。あなたが黙秘すると利得は－10、自白すると－5になりますので、自白を選びます。○を付けておきましょう。

 

次に相棒を考えます。あなたが黙秘した場合（利得表の上半分）、相棒が黙秘すると利得は－3、自白すると－1になるので、相棒は自白を選びます。相棒の利得の下に△を付けておきます。あなたが自白した場合に相棒が黙秘すると利得は－10、自白すると利得は－5になるので、相棒は自白を選びます。

 

マークを付けた利得表は以下のようになります。

 

 

○と△が両方とも付いているところがゲームの解となります。ゲームの解はナッシュ均衡ともいいます。右上や左下のように○と△のうち1つだけのところは、ゲームの解にはなりません。

 

◆囚人のジレンマの特徴

このゲームの解にはいくつかの特徴があります。まずは、ゲームの解が1つあるということです。ゲームの解がどこになるのかは利得表の数値次第です。数値によってゲームの解は0から2つになりますが、囚人のジレンマではゲームの解は1つです。

 

次は、ゲームの解が支配戦略均衡になっているということです。相手がどの戦略を選んだとしても自分の戦略が1つに決まることを支配戦略といいます。囚人のジレンマでは2人とも自白という支配戦略を持っており、このようなゲームの解を支配戦略均衡といいます。

 

最後は、ゲームの解がパレート最適ではないということです。このゲームでは明らかに（自白、自白）よりも（黙秘、黙秘）の方がいい結果になります。プレイヤーは互いに利得表を知っているにもかかわらず、2人とも（黙秘、黙秘）を選択しようとしていません。2人が合理的に行動しているにもかかわらず、その結果は望ましいものにならないのが囚人のジレンマの最大の特徴です。

 

 

◆支配戦略のないゲーム

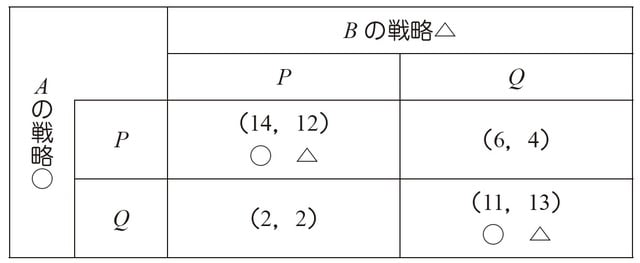
次の利得表を使ってナッシュ均衡のルールでゲームを解いてみましょう。

 

 

・Aの戦略

BがP　→　AはP

BがQ　→　AはQ

 

・Bの戦略

AがP　→　BはP

AがQ　→　BはQ

 

となるため、ゲームの解は（P, P）と（Q, Q）の2つになります。このゲームには、ゲームの解は2つ、支配戦略がない、ゲームの解はパレート最適になっている、という特徴があります。

 

このタイプのゲームは逢引のジレンマとも呼ばれます。AとBがどこで逢引（デート）するのかを決めるゲームですが、2人が別々の場所に行くのは意味がなく、利得が低くなっています。逢引のジレンマでは、AとBのどちらが交渉力が強いのかなど他の要素がないとゲームの解が1つに決まりません。

 

 

川野 祐司
東洋大学　経済学部国際経済学科　教授