宝くじに「期待値」を使うとどうなるか？

将来を予測し、結果によって得られる成果が変わってくるような状況の最たるものといえば、そう、ギャンブルですね。歴史上の数学者にもギャンブル好きな人はいたようで、そのことで確率論が飛躍的に発展したなんてこともいわれています。

というわけで、ここでは期待値の考え方を使って、ギャンブルを分析していきましょう。

誰もが知っているギャンブルの1つに「宝くじ」があります。今回は宝くじを例に考えてみましょう。

この原稿を書いているのが11月なのですが、ちょうど「年末ジャンボ宝くじ」が発売中です。これを例にすることにしましょう。

公式サイトを見ると、2022年の「年末ジャンボ宝くじ」の当せん金と本数は、下の［図表1］のようになっていました。

［図表1］「年末ジャンボ宝くじ」の当せん金と本数

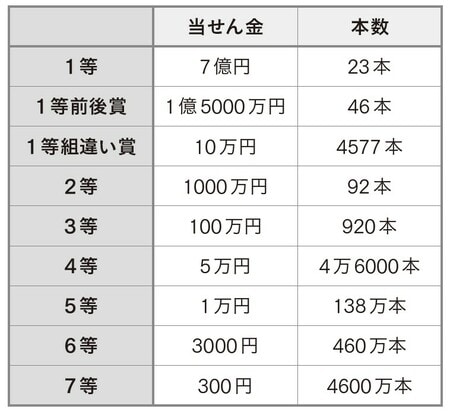
発売予定枚数は4億6000万枚とあったので、これを採用しましょう。

さて、この宝くじの期待値はいくらになるのでしょう？

なお、この宝くじの購入金額は1枚300円でした。当然期待値はこれより小さくなるはずですね。でないと宝くじの運営自体が成り立ちませんから。

さて、この宝くじの期待値はいくらに設定されているのでしょう？

まず、1等が出る確率です。全部で4億6000万枚のくじがあり、その中で1等くじが23本入っているわけですので、1等が当たる確率は、「23枚／4億6000万枚＝1／2000万（2000万分の1）」という計算になります。

2022年現在で日本全国に住む40〜50歳の人口が約2000万人だそうです。ですので、日本中の40〜50歳の人が全員1枚ずつ宝くじを買って、その中の1人が当たる計算になります（笑）。

それ以外の賞についても同様に当せん確率を計算した結果が、［図表2］のようになります。

［図表2］「年末ジャンボ宝くじ」当せん確率

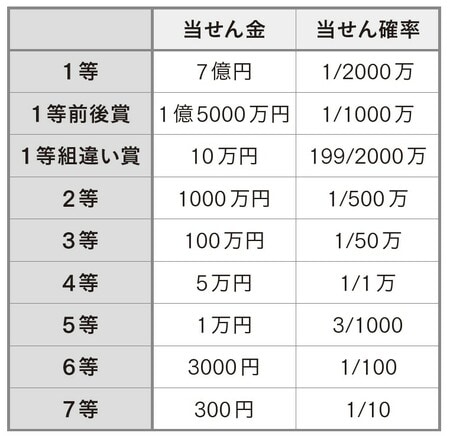
■エクセルで宝くじの期待値を計算する

では、いよいよ期待値の計算に入りましょう。期待値とは、それぞれの等について「当せん金×当せん確率」を計算し、それらをすべて足せば導き出せます。

では、エクセルに登場してもらいましょう。