超便利! エクセルを使った「期待値」の計算
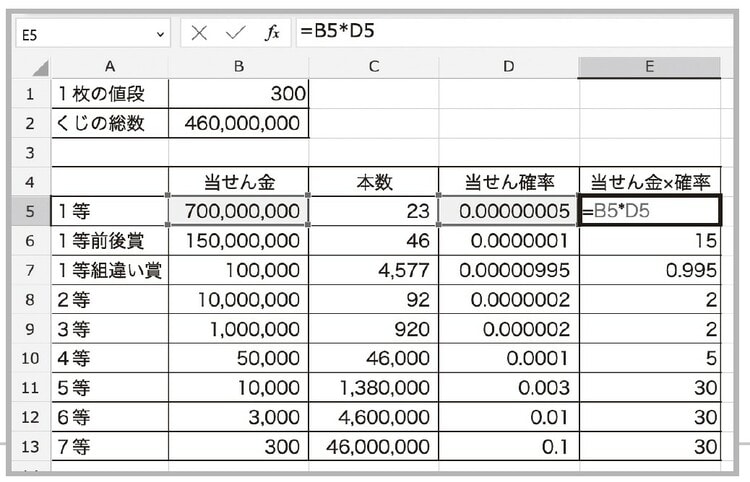
1.B1に宝くじ1枚の購入金額(300)、B2にくじの枚数(4億6000万)、B5からB13の列に各賞の当せん金、C5からC13に各賞の当せん本数を入力しています。
2.D列には当せん確率を入れています。計算方法は、先ほど示したとおりです。
たとえば1等の当せん確率(D5)は、「1等の本数(C5)/くじの総数($B$2)」の計算式を入れています。結果は2000万分の1(小数にすると0.00000005)になります。
これをオートフィルでコピーして、7等までの当せん確率をD列に計算しています。
3.次はE列の「当せん金×確率」のセルを埋めましょう。たとえば1等の場合は、[図表3]にあるようにE5のセルに「=B5(当せん金)*D5(当せん確率)」と入力すればOKです。
4.これも7等(E13)までオートフィルでコピーしましょう。
5.あとは、E5からE13までの数値をすべて足せば期待値が計算できます。これには足し算を行なうSUM(サム)関数を使いましょう。
E14に「=SUM( 」として範囲(E5からE13)を指定してもよいですし、オートSUMを使えば自動的に計算してくれるので、そちらを使ってもよいでしょう。
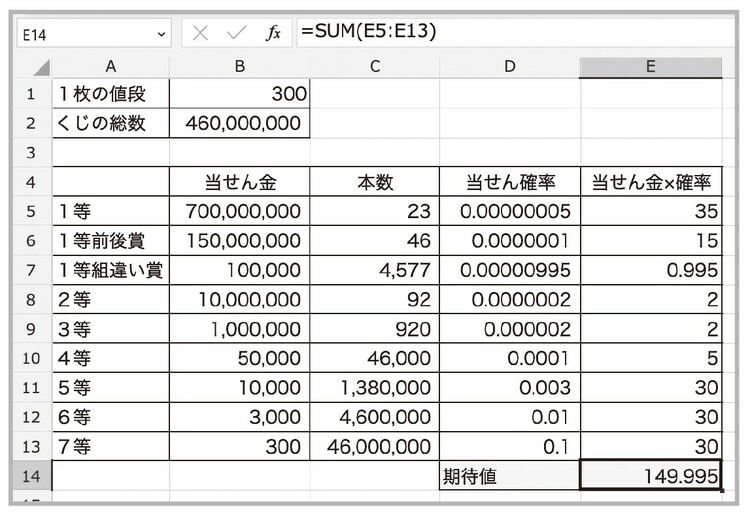
すると結果は約149.995円と出ました。これが2022年の年末ジャンボ宝くじの期待値というわけです。つまり、「1枚買えばだいたい150円、つまり半分ぐらいの賞金が当たる」と期待できる、ということです。
このように期待値は、その意味とエクセルの使い方を知っておけば、意外とカンタンに自分で計算することができます。
なお、「ジャンボ宝くじ」の期待値はどれもくじの値段の49〜50%に設定されているようです。またスクラッチ式のくじや「ロト6」のような数字を選ぶくじの期待値は約45%になっています。
ですので、どちらを買おうか迷っている人は、ジャンボ宝くじのほうが期待値が大きい、ということは知っておいていいかもしれません。
世の中は確率で溢れています。気になる確率があれば、その期待値を計算してみると面白いかもしれません。そしてその感覚は、きっと自身の仕事にも活きてくるはずです。
鈴木 伸介
株式会社数学アカデミー 代表取締役
































