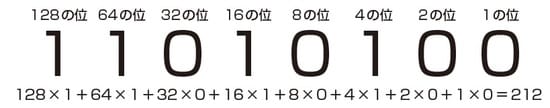十六進法で「2B3」を十進法で表すと、いくつになる？

 

 

N進法は「位取り記数法」とも呼ばれる

私たちが、普段から何気なく使っている数字は、「位取り記数法（くらいどりきすうほう）」という方法で表したものです。ローマ数字とは異なり、「位」という考え方が用いられています。「位取り記数法（くらいどりきすうほう）」のことを、「N進法」とも言います。

 

10個集まると次の位になる数の表し方を、十進法と言います。

 

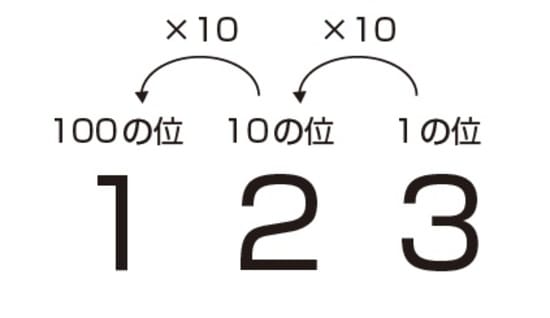
「1の位」に10個集まると、10倍された「10の位」になり、「10の位」に10個集まると、さらに10倍された「100の位」へと位があがります。

 

十進法では、0を含めて10種類の記号が必要となります。十進法で「123」と表すと、「100の位」が1、「10の位」が2、「1の位」が3というように考えますよね。

 

式で表すと、100×1＋10×2＋1×3となります。

数が16個集まると位があがる「十六進法」

10個ではなく、16個集まると位があがる形で数を表すこともできます。これを十六進法と言います。

 

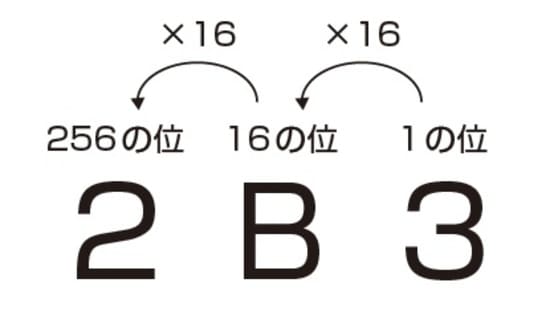
この時、「1の位」の次は16倍された「16の位」、その次の位はさらに16倍された「256の位」となります。

 

十六進法では、0を含めて16種類の記号が必要となるので、0～9に加え、「A，B，C，D，E，F」を用います。それぞれ十進法に直すと、Aは10、Bは11、Cは12、Dは13、Eは14、Fは15となります。

 

十六進法で「F」が1文字あるだけで、十進法の「15」となるのは不思議に感じるかもしれませんが、まずは「そういうものだ」と思っておきましょう。

 

たとえば、十六進法で「2B3」と表すと、「256の位」が2、「16の位」がB、「1の位」が3となるわけです。

 

十進法に直すと、256×2＋16×11＋1×3＝691となります。このように、十進法以外で表された数を十進法に直すのは、各位が何を表しているかを考えていけば、簡単ですね。

 

二進法や十六進法は、とくにコンピュータで数字を扱う時に便利な方法です。そのため、非常によく使われています。

十進法以外で表された数を、十進法にしてみよう

次に、十進法以外の数を十進法に直す練習をしてみましょう。

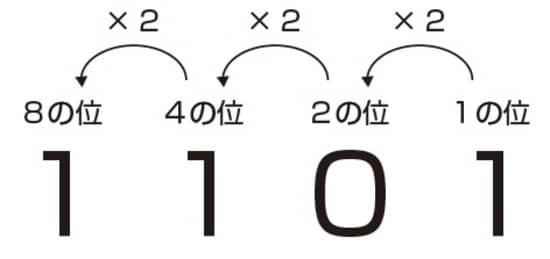
二進法では、2個集まると次の位になるので、下の位から順に1の位、2の位、4の位、8の位となります。

よって、（1）の答えは、8×1＋4×1＋2×0＋1×1＝13となります。

 

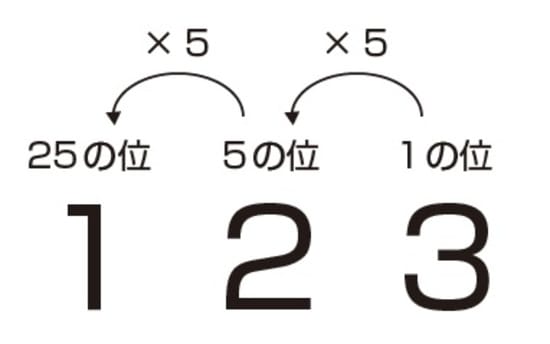
五進法では、5個集まると次の位になるので、下の位から順に1の位、5の位、25の位となります。

よって、（2）の答えは、25×1＋5×2＋1×3＝38となります。

十進法から別のN進法に数字を直す

では、続いて、十進法から別のN進法に数字を直してみましょう。例として、123（十進法）を二進法で表すことを考えます。

 

1の位から、順を追って位をあげていきます。2個集まると位があがるので、123÷2＝61あまり1と計算することで、「2の位」が61、「1の位」があまりの1となります。

 

123＝2×61＋1×1

 

「2の位」に61個も集めることはできないので、さらに位をあげます。61÷2＝30あまり1と計算することで、「4の位」が30、「2の位」があまりの1となります。

 

123＝4×30＋2×1＋1×1

 

「4の位」の30個について、30÷2＝15あまりなしと計算することで、「8の位」が15、「4の位」が0とできます。

 

123＝8×15＋4×0＋2×1＋1×1

 

この作業を繰り返すと、123を次のように表すことができます。

 

123＝64×1＋32×1＋16×1＋8×1＋4×0＋2×1＋1×1

 

これで、123（十進法）を二進法で表すと、「1111011」となることがわかりました。

 

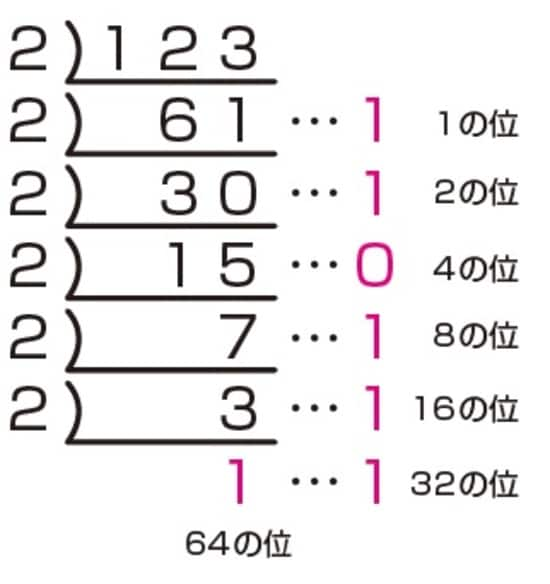
十進法の123を二進法に直す計算について、割り算の式を書くと、次のようになります。

 

式をたくさん書くのは大変ですが、割り算を筆算でつなげて書くと、少しラクに計算できます。

ちなみに、二進法で「1111011」と表された時、10の位や100の位ではないので「ヒャクジュウイチマンセンジュウイチ」とは読みません。単に「イチイチイチイチレイイチイチ」と読むようにしてください。

 

 

では、練習してみましょう。

 

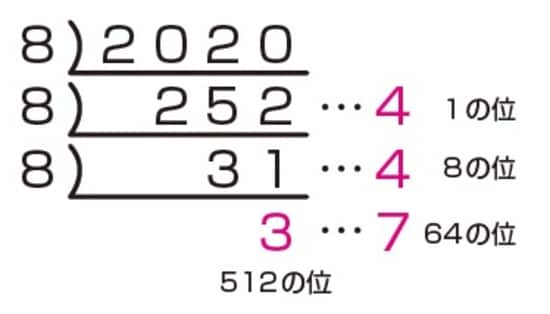
（1）の問題の2020を、十進法から八進法に直すには8で割り続けます。

 

これで、2020は八進法だと3744となることがわかりました。（2）の問題ですが、二進法から十六進法に直接変換（へんかん）するのは難しいので、まずは十進法に直しましょう。

二進法で表された11010100を十進法に直すと212となることがわかりました。16で割り算して、十六進法に直しましょう。この計算はすぐに終わります。

 

13は十六進法では「D」と表すことになっているので、212を十六進法に直すと、D4となります。

 

 

松本 亘正
中学受験専門塾ジーニアス　代表

教誓 健司
中学受験専門塾ジーニアス　講師

 

【関連記事】

■税務調査官「出身はどちらですか？」の真意…税務調査で“やり手の調査官”が聞いてくる「3つの質問」【税理士が解説】

 

■月22万円もらえるはずが…65歳・元会社員夫婦「年金ルール」知らず、想定外の年金減額「何かの間違いでは？」

 

■「もはや無法地帯」2億円・港区の超高級タワマンで起きている異変…世帯年収2000万円の男性が〈豊洲タワマンからの転居〉を大後悔するワケ

 

■「NISAで1,300万円消えた…。」銀行員のアドバイスで、退職金運用を始めた“年金25万円の60代夫婦”…年金に上乗せでゆとりの老後のはずが、一転、破産危機【FPが解説】

 

■「銀行員の助言どおり、祖母から年100万円ずつ生前贈与を受けました」→税務調査官「これは贈与になりません」…否認されないための4つのポイント【税理士が解説】