検索
人間が美しさを感じる「黄金比」
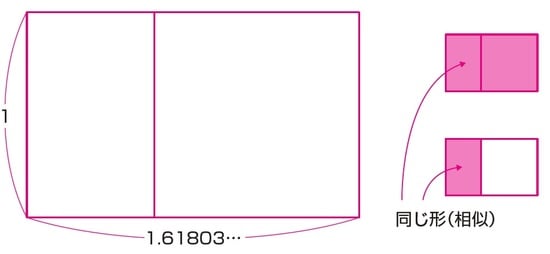
さて、下の図のように、長方形から正方形を切り取ると、もとの長方形と同じ形（相似）になる長方形があるとします。
このような長方形の縦と横の長さの比を、「黄金比」と言います。簡単な整数の比で表すことはできませんが、短いほうの辺の長さを1とすると、「1：1.61803…」となります。
黄金比は、およそ「1：1.618」とされることが多いのです。これは人間が美しさを感じる比率と言われていて、美術品や建物の中に多く見出すことができます。古代ギリシアの時代に建てられたパルテノン神殿が、その一例として有名です。
連続するフィボナッチ数の関係は、黄金比に近づく
じつは、前回の記事（灘、開成に入る子なら解ける「フィボナッチ数列」の問題とは？）に掲載していた例題のように正方形をたくさん描いていくと、全体の長方形の縦と横の長さの関係が「黄金比」に近づいていくことが知られています。
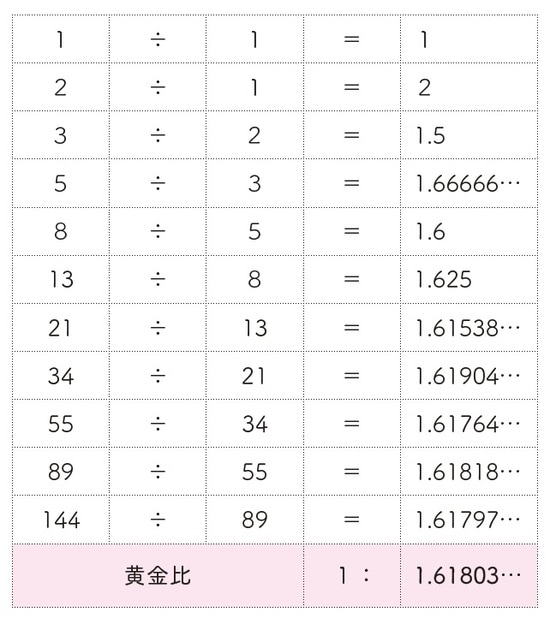
本当に黄金比に近づいていくのか、さっそく計算してみましょう。フィボナッチ数列について、次の数が前の数の何倍になっているのかを計算すればいいですね。
順番に割り算してみると、次のようになります。
このように、少しずつ黄金比に近づいていくのです。この法則を知ると、きっとフィボナッチ数列を見るたびに「美しい」と感じるようになっていくはずですよ。
フィボナッチ数列の総まとめ
●1番目の数を1、2番目の数を1として、
3番目の数＝1番目の数＋2番目の数＝1＋1＝2
4番目の数＝2番目の数＋3番目の数＝1＋2＝3
というように前の2つの数を足した数を並べたものを「フィボナッチ数列」と言う
1，1，2，3，5，8，13，21，34，55，89，144，233，…
●フィボナッチ数列に登場する数を「フィボナッチ数」と言う
●フィボナッチ数は、自然界でも多く確認することができる数
●連続する２つのフィボナッチ数の関係は、「黄金比」（およそ1：1.618）に近づいていく
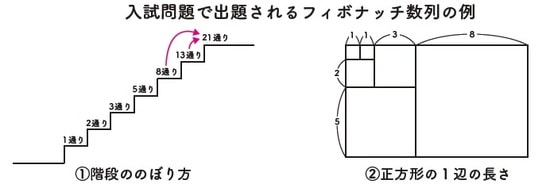
① は、一度に1段または2段で階段をのぼる方法の計算問題
②は、1辺の長さが1の正方形を2つ並べて長方形をつくり、そのすぐ下、そのすぐ右へと、順番に接する正方形を並べていく時の正方形の1辺の長さの計算問題
●フィボナッチ数列のように、前の数を組み合わせて次の数が決まるような問題を解く時には、まずは小さい数で計算をしながら規則を見つけて、その規則を使って大きな数の計算をしていくのがポイント
松本 亘正
中学受験専門塾ジーニアス 代表
教誓 健司
中学受験専門塾ジーニアス 講師
【関連記事】
■税務調査官「出身はどちらですか？」の真意…税務調査で“やり手の調査官”が聞いてくる「3つの質問」【税理士が解説】
■月22万円もらえるはずが…65歳・元会社員夫婦「年金ルール」知らず、想定外の年金減額「何かの間違いでは？」
■「もはや無法地帯」2億円・港区の超高級タワマンで起きている異変…世帯年収2000万円の男性が〈豊洲タワマンからの転居〉を大後悔するワケ
■「NISAで1,300万円消えた…。」銀行員のアドバイスで、退職金運用を始めた“年金25万円の60代夫婦”…年金に上乗せでゆとりの老後のはずが、一転、破産危機【FPが解説】
■「銀行員の助言どおり、祖母から年100万円ずつ生前贈与を受けました」→税務調査官「これは贈与になりません」…否認されないための4つのポイント【税理士が解説】
