中学受験では、灘、開成、麻布といった超難関校ほど「数の性質」の単元が入試に多く出る傾向があります。この単元は、「わかる」と「正解する」のギャップが大きくなりやすいため、注意が必要です。難関校合格のために不可欠な単元の学習方法を紹介します。
教誓先生:読み方は「きょうせい せんせい」。名は体を表すのか、教えることが大好き。幼い頃から約数の多い数は「よい」数だと感じていたが、あまり共感を得られないらしい。出題者の意図をくんで解くことを心掛けている。
まなぶ君:算数は好きだけど、勉強は嫌いで、できればラクしたいと思っている小学5年生。6年生になったら中学受験をするので塾に通っている。たまにめんどくさがり屋の一面をのぞかせる。
美しい創作はすべて約1.618倍の比率…これって偶然?
教誓先生:さあ、今日もがんばりましょう。ところで、もっとも美しい形はどのような形だと思いますか?
まなぶ君:唐突ですね…やっぱり正三角形や立方体かなぁ。
教誓先生:確かに、図形の問題を解く時に、正三角形や正方形、立方体といった美しい形を考えると、解き方が見えてくることがあります。とても大事な視点です。でも、今日はちょっと違う話です。質問を変えましょう。ルーブル美術館には、「モナリザ」という絵があります。この絵に描かれている女性の顔の縦の長さは横の長さの何倍でしょう?

まなぶ君:そんなのわかるわけないですよ。じゃあ2倍!
教誓先生:2倍もあると思いますか? それじゃあ、顔が長すぎますよ。
まなぶ君:確かに…。じゃあ、1.5倍!
教誓先生:正解は…約1.618倍です。
まなぶ君:先生、ぼくはクイズ選手権に出るつもりはないので、そういう雑学を教えてもらってもあまり意味がないような…。
教誓先生:パリに行くと、「モナリザ」以外にも約1.618倍の比率のものをたくさん見つけることができるんですよ。同じルーブル美術館にある「ミロのヴィーナス」もそうです。他に「凱旋門(がいせんもん)」にも同じ比率がありますね。
まなぶ君:そういえば、先生はパリが好きで何回も旅行に行っているんでしたっけ。でも、ぼくにとってはどうでもいい情報だなぁ。だいたい、1.618倍というのも偶然かもしれないし…。そろそろ算数の勉強を始めましょうよ。
教誓先生:えぇ、もう始まっていますよ。
まなぶ君:えっ⁉
フィボナッチ数列は、1つ前の数が足されていく数列
まずは、次の問題を見てみましょう。
ある規則にしたがって、数が並んでいます。
1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, □
この時、□にあてはまる数を求めなさい。
この数列は、中学入試によく登場する有名な数列です。6年生の受験生であれば、瞬間的に反応できなくてはいけません。いったいどんな規則があるのでしょうか。まずは差に注目します。

差を書き込んでみると、どんな規則があるか見えてきましたね。前の2つの数を足す形になっています。
よって、答えは89+144=233と求めることができます。
このような数列を「フィボナッチ数列」と言い、この数列に登場する数をフィボナッチ数と言います。1202年に出版された『算盤(そろばん)の書』の中で紹介されていて、その筆者であるレオナルド・フィボナッチの名前が使われています。
植物の花びらにも隠れているフィボナッチ数
フィボナッチ数は、自然界の至るところで発見できることが知られており、花びらの枚数はフィボナッチ数であるものが多いようです。たとえば、ユリの花びらは3枚、サクラの花びらは5枚、コスモスの花びらは8枚になっています。
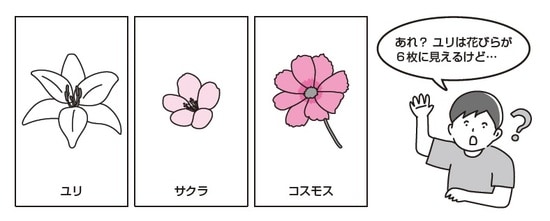
ユリの花びらは一見6枚に見えますが、外側にある3枚の花びらのようなものは、「がく」です。同じように、「がく」が「花びら」と間違えられやすい植物としてはアジサイが有名ですね。
『種の起源』の著者であるイギリスの科学者ダーウィンが体系化した「自然選択説」という考え方があります。これによると、自然環境に適した生き物のほうが子孫を残しやすいようです。
花びらが7枚の植物よりも、フィボナッチ数である8枚のほうが自然環境に適しているとしたら、何とも不思議なものですね。
※次回は、次回は、難関中学の入試問題によく取り上げられる数式の問題を例に、さらに詳しく解説していきます。
松本 亘正
中学受験専門塾ジーニアス 代表
教誓 健司
中学受験専門塾ジーニアス 講師




























