中学受験では、灘、開成、麻布といった超難関校ほど「数の性質」の単元が入試に多く出る傾向があります。この単元は、「わかる」と「正解する」のギャップが大きくなりやすいため、注意が必要です。難関校合格のために不可欠な単元の学習方法を紹介します。
階段の上り方に規則性…実は背後にあの数列が⁉
フィボナッチ数はさまざまな問題の背後に隠れています。
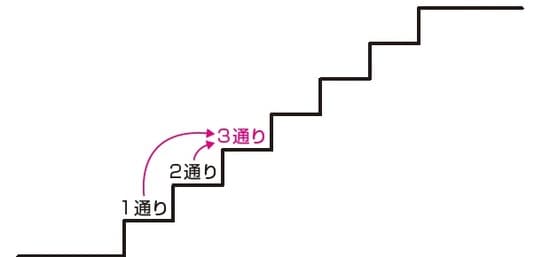
階段を一度に1段または2段のぼります。その時、2段の階段をのぼる方法には、1段ずつ2回でのぼる方法と、2段を1回でのぼる方法の2通りがあります。7段の階段をのぼる方法は何通りありますか。
まずは、「場合分け」をして地道に数えてみましょう。1段と2段を組み合わせて7段にする方法は、次の4パターンがあります。
パターン①……7=1+1+1+1+1+1+1
パターン②……7=1+1+1+1+1+2
パターン③……7=1+1+1+2+2
パターン④……7=1+2+2+2
「1+1」を「2」と入れ替えていくことで、もれのないように書き出すことができます。
パターン①は、並べ替えても1通りです。
1+1+1+1+1+1+1
パターン②を並べ替えると、全部で6通りあります。
1+1+1+1+1+2
1+1+1+1+2+1
1+1+1+2+1+1
1+1+2+1+1+1
1+2+1+1+1+1
2+1+1+1+1+1
パターン③を並べ替えると、全部で10通りあります。
1+1+1+2+2
1+1+2+2+1
1+1+2+1+2
1+2+2+1+1
1+2+1+2+1
1+2+1+1+2
2+2+1+1+1
2+1+2+1+1
2+1+1+2+1
2+1+1+1+2
パターン④を並べ替えると、全部で4通りあります。
1+2+2+2
2+1+2+2
2+2+1+2
2+2+2+1
これらをすべて合計すると21通りになります。21はフィボナッチ数でしたね(前回の記事『わかっても、正解できない…超難関中学入試「数の性質」の問題』参照)。
隠れているフィボナッチ数列の見つけ方
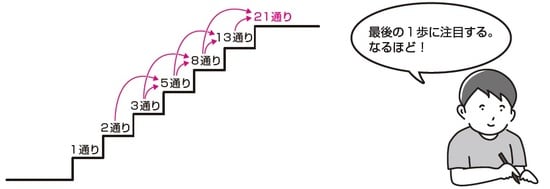
次のように考えると、段数がもっと増えても簡単に求めることができます。
1段の階段をのぼる方法が1通りで、2段の階段をのぼる方法が2通りということはすぐにわかります。
3段の階段をのぼる時の最後の1歩に注目すると、1段目から2段のぼるか、2段目から1段のぼるかのどちらかになります。そうすると、3段のぼる方法が1+2=3通りと求めることができます。
4段の階段をのぼる場合も、最後の1歩に注目すると、2段目から2段のぼるか、3段目から1歩のぼるかのどちらかになります。そうすると、4段のぼる方法は2+3=5通りということがわかります。
この作業を繰り返していくと、次のように計算できます。
・5段のぼる方法は、3+5=8通り
・6段のぼる方法は、5+8=13通り
・7段のぼる方法は、8+13=21通り
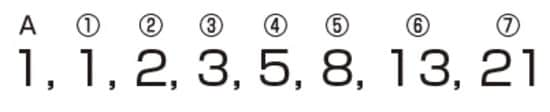
このように、フィボナッチ数列が隠れていたことがわかりましたか? 1段から何通りかを順に並べると、{1,2,3,5,8,13,21}となります。ここから先についても、前の2つの数を足し算することで次の数が求められるようなしくみがあることが確認できたので、フィボナッチ数列が続いていくことがわかります。
今回のように、まずは小さい段数で計算をしてみて、そこで何か規則を見つけて、その規則を使ったもっと大きな段数について計算していく…という姿勢は、さまざまな問題を解いていくうえでとても大切です。
敷きつめた正方形…辺の長さを求めてみると
続いて、次の問題を解いてみましょう。
1辺の長さが1㎝の正方形Aがあります。図のように、Aと1辺を接する正方形①をAの右へ描いて長方形をつくり、次に、その下へ1辺を接する正方形②を描いて長方形をつくります。さらに、その右へ正方形③を描いて長方形をつくります。
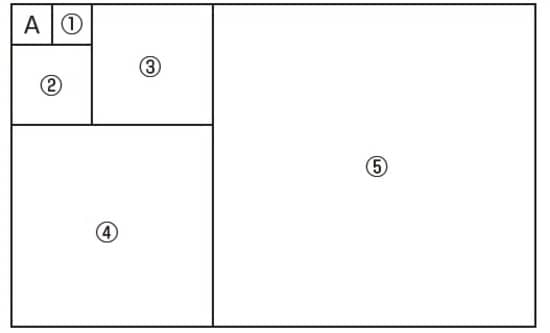
この操作を繰り返し行う時、正方形⑦の1辺の長さは何㎝ですか。
図を見ながら、順番に長さを求めてみましょう。
①の1辺の長さは、1㎝
②の1辺の長さは、1+1=2㎝
③の1辺の長さは、1+2=3㎝
④の1辺の長さは、2+3=5㎝
⑤の1辺の長さは、3+5=8㎝
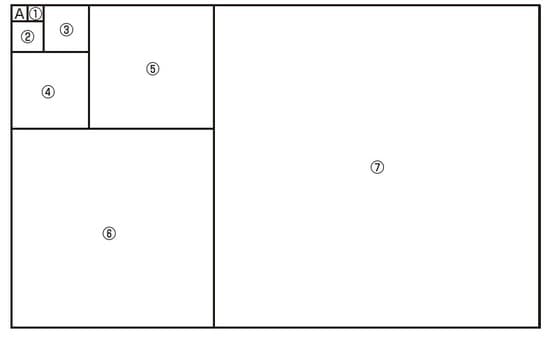
続きの図を描くと、次のようになります。
図形を見れば、新しく正方形を描いた時には、1つ前の正方形と2つ前の正方形の1辺の長さの和になっていることが確認できますね。
⑥の1辺の長さは④と⑤の和に、⑦の1辺の長さは⑤と⑥の和になっています。
⑥の1辺の長さは、5+8=13㎝
⑦の1辺の長さは、8+13=21㎝
ここでは足し算の式をすべて書きましたが、実際に問題を解く時は、正方形の1辺の長さだけを、数列として書き出すほうがよいでしょう。途中までは、実際に図の中に数字を書き込みながら考え、規則に気づいたあとは数字だけを書いていく流れをつくりましょう。
フィボナッチ数からできあがる「黄金螺旋」
ちなみに、この正方形を順番に描いていく作業を、右→下→右→下ではなく、右→下→左→上と輪を描くように並べると、おもしろい形ができます。正方形をたくさん並べて、外側の正方形から順番に弧(こ)を描いていくと、次の図のようになります。
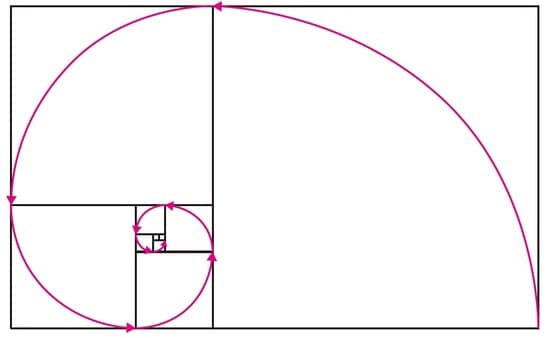

このような渦(うず)は、「黄金螺旋(らせん)」と呼ばれていて、これもまた自然界で数多く目にすることができます。このような模様のある生き物を、見たことがありませんか?
松本 亘正
中学受験専門塾ジーニアス 代表
教誓 健司
中学受験専門塾ジーニアス 講師
【関連記事】
■税務調査官「出身はどちらですか?」の真意…税務調査で“やり手の調査官”が聞いてくる「3つの質問」【税理士が解説】
■親が「総額3,000万円」を子・孫の口座にこっそり貯金…家族も知らないのに「税務署」には“バレる”ワケ【税理士が解説】
■「銀行員の助言どおり、祖母から年100万円ずつ生前贈与を受けました」→税務調査官「これは贈与になりません」…否認されないための4つのポイント【税理士が解説】