電卓に隠された「2220」のミステリー

なぜか答えは「2220」

電卓には、いくつもの面白い計算が隠されています。そのうちの一つをご紹介しようと思います。皆さんもお手元に電卓をご用意ください。

 

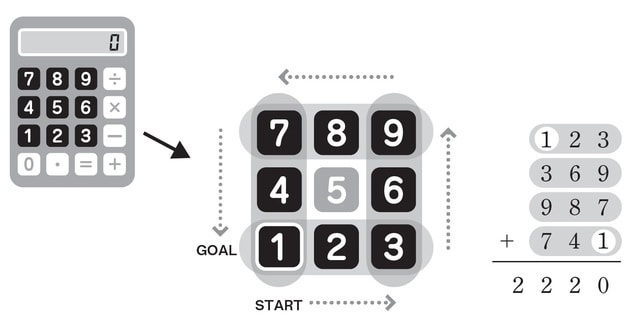
電卓の数字キーは「1」から反時計回りに「2、3、6、9、8、7、4」と並んでいます。

 

この順番通りに並んだ三つの数字を三桁の数として、四つの数をつくっていきましょう。「1」から始めて「1」に戻る足し算をしてみると、「123+369+987＋741」と足していくということです。

 

そうすると、答えは「2220」になります。

 

それでは、次に「2」から始めて「2」に戻る足し算をしてみましょう。「236+698+874+412＝2220」というように、やはり結果は「2220」となります。

 

 

同じように、スタートの数字が「3」「6」「9」「8」「7」「4」の場合についても足し算をしてみてください。

 

面白いことに結果はすべて「2220」になります。

 

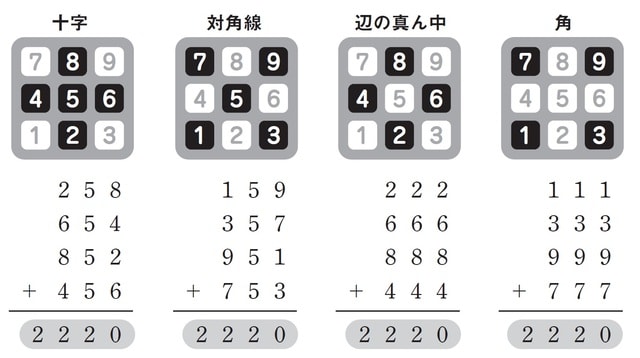
次は、角の数（1、3、9、7）を、それぞれ三回押した数（三桁ずつ）の足し算をしてみましょう。「111+333+999+777」。

 

やはり結果は「2220」です。

 

辺の真ん中の数（2、6、8、4）を三桁ずつ足し算してみましょう。「222+666+888+444」。やはり結果は「2220」です。

 

では、対角線の三つの数字を三桁の数として、四つの数を足し算してみると、どうでしょうか。「159+357+951+753＝2220」。またもや「2220」です。

 

最後に十字の三つの数字を三桁の数として、四つの数を足し算します。「258+654+852+456＝2220」。なんとこれも「2220」です。

 

 

読者の皆さんも、電卓を片手に「ぐるっと一回りの足し算」、そして「角」「辺の真ん中」「対角線」「十字」の足し算を試してください。その次に、計算を紙に書いて、足し算を確かめてみてください。

 

どうしてすべての足し算が「2220」になってしまうのか──。紙に書いた計算をもとに、その謎に迫りましょう。

「2220」の謎解きは手計算の後で

 

 

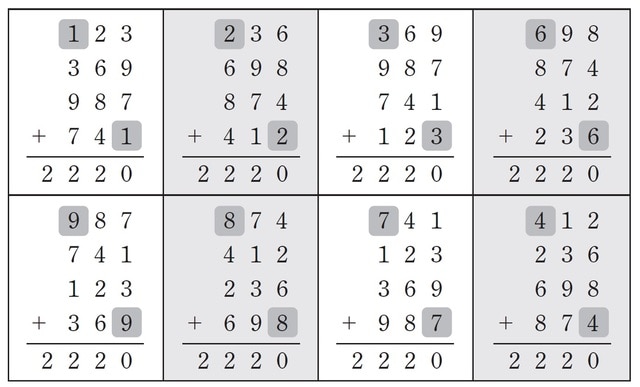
まずは「ぐるっと一回りの足し算」です。電卓の数字キーは「1」から反時計回りに「2、3、6、9、8、7、4」と並んでいます。同じように、「2、3、6、9、8、7、4」のそれぞれから始めて足し算をします。この八つの計算をよく眺めてください。

 

結果はいずれも「2220」です。しかも、出現する順番は違っても、「123、369、987、741」を足す計算と、「236、698、874、412」を足す計算の二種類に分類されることがわかります。

 

次に、別の四つの足し算を紙に書いてみましょう。

 

数字キーの角の四つの数字でつくった三桁の数を足し合わせた「角」。辺の真ん中にある四つの数字でつくった三桁の数を足し合わせた「辺の真ん中」。対角線に並ぶ三桁の数字を足し合わせた「対角線」。十字に並ぶ三桁の数字を足し合わせた「十字」です。

 

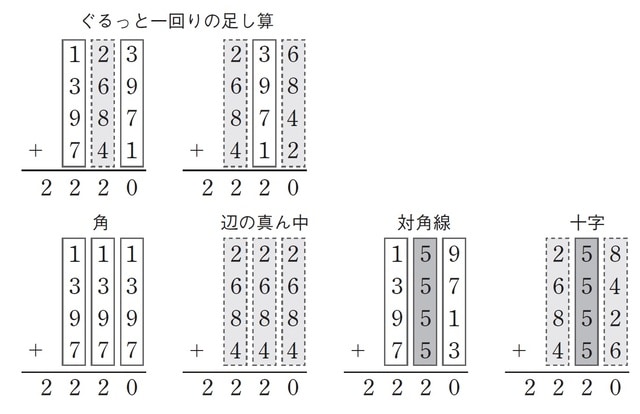
ここで、「ぐるっと一回りの足し算」の二種類と後の四種類のあわせて六種類の計算を縦方向に眺めてみてください。

 

 

ある法則に気づきませんか？　すべての計算は「1、3、9、7の列」「2、6、8、4の列」、そして「5、5、5、5の列」の三種類でできていることがわかります。そして、この三種類の列の合計はすべて「20」となり、等しい値となるのです。

 

つまり、六種類の足し算はいずれも「百の位も20」「十の位も20」「一の位も20」になるということです。これを足し合わせると「20×100+20×10+20×1＝2220」となります。

 

こうして、六種類の計算はいずれも合計が「2220」となるのです。つまり、一見異なる「十二通りの足し算」は、分類していくことで、どれも合計が「2220」になる理由がわかります。

 

 

桜井 進

株式会社sakurAi Science Factory　代表取締役