天才オイラーよりも早い発見

[図1]発微算法演段諺解

建部賢弘の業績の中でも世界的に注目されている「円周率π」の計算について紹介しましょう。

建部の師・関孝和は「正131072（＝217）角形」から、円周率を小数第16位まではじき出しました。

この計算のポイントは今日では「エイトケン加速」とよばれている計算法（「増約術」）を用いたことです。これは少ない演算で、桁数の多い正確な数値を得るための計算手法です。

円周率の計算の場合には、「直径1」の円に内接する正多角形の周の長さを計算することで正確な値を求めていくことになります。

「正2ⁿ角形」の「n」を一つずつ増やしていくときには、周の長さの数値をどれだけ正確に求められるかがカギになります。関孝和は「n」を一つずつ増やしていくと、周の長さが等比数列になるという法則を見つけたのです。

これに対して建部賢弘は、円周の数列の中に新たな法則を見つけることに成功しました。建部が見つけた法則は「累遍増約術」とよばれる「加速法」です。

現在では、「リチャードソン加速」といわれているこの計算により、建部は「正1024（＝210）角形」から円周率を小数第42位をはじき出すことに成功しました。ちなみに、円周率計算において、「リチャードソン加速」は二十一世紀になっても研究されているテーマです。

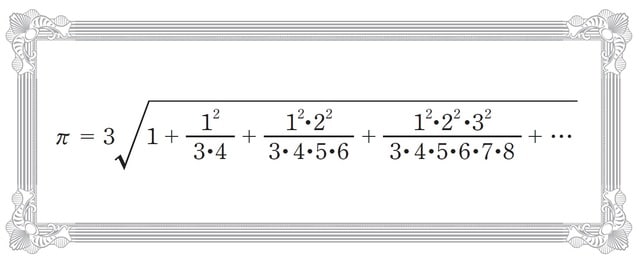
次頁の図をご覧ください。これが、一七二二年『綴術算経』の中で建部賢弘が示した円周率の公式です。

[図2]建部賢弘が示した円周率の公式

この「無限級数」の公式は、「三角関数sin」の逆三角関数である「arcsin（アークサイン）」を「テイラー展開」した公式に、「x＝1／2」を代入した公式だったのです。

驚くべきことに、この公式は天才レオンハルト・オイラーが微積分学を用いて同じ公式を発見する十五年前のことでした。

このように建部賢弘の数学は、円周率一つをとってみても、世界に誇れる成果を残しています。鎖国をしていた江戸時代、日本の数学は独自に発展しながらも、世界の数学と肩を並べるレベルに達していたのです。そこに、和算の奥深さがあります。

[図3]逆三角関数arcsinを「テイラー展開」した公式

将軍吉宗も建部を評価

一七一三年、徳川家継が七代将軍となり、建部は家継に仕えることになりました。しかし、家継は、わずか在位四年で没してしまいます。

続いて吉宗が八代将軍となると、慣例通りに、前将軍家継の家臣は揃って引退しました。建部も引退するはずでしたが、吉宗は彼を江戸城によび戻したのです。

その目的は、改暦にありました。建部は、『算暦雑考』『極星測算愚考』『授時暦議解』といった書を著し、天文、暦算の顧問役を果たしました。

結果として、三代の将軍に仕えることになりましたが、これは江戸時代にあっては大変に珍しいことです。いかに将軍家が建部賢弘の才能を買っていたかがわかりますね。

桜井 進

株式会社sakurAi Science Factory　代表取締役