計算術の奥は深い！

両手を使う計算術その1　掛け算九九　九の段　9×3

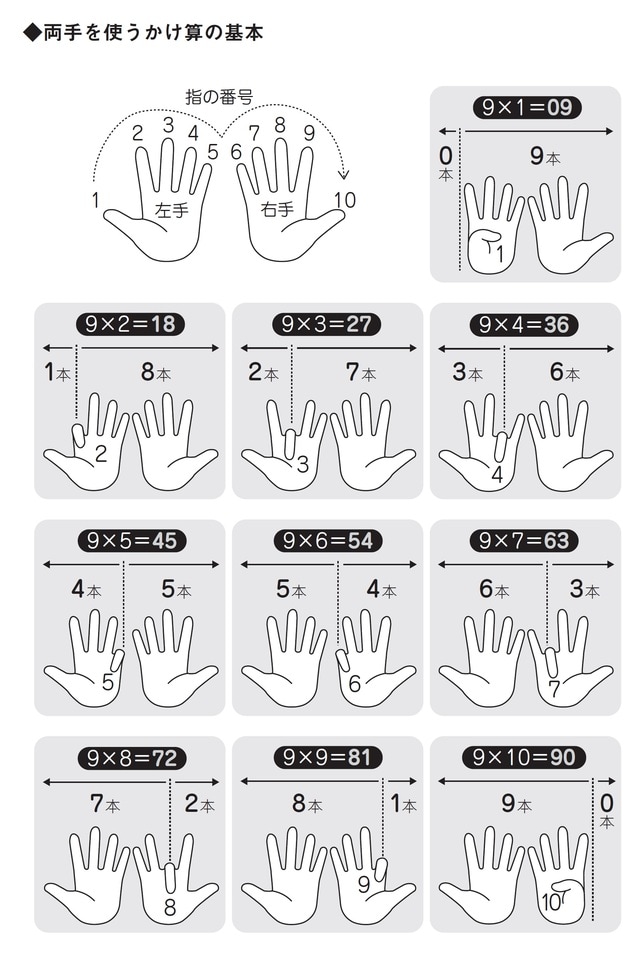
かけ算九九の九の段は両手を使って簡単に計算できます。

 

まず手の裏を自分にみせて両手をそろえます。次に9×〇ならば左から〇本目の指を折ります。

 

9×③であれば、左から③本目の指を折ります。すると、折った指の左側に立っている指は2本、右側に立っている指は7本となりますが、それぞれ9×3の十の位と一の位の数となるので答えは27とわかります。

 

9×8であれば、左から8本目の指を折ります。折った指の左右の指の数はそれぞれ7本と2本なので72ということです。

 

9×1の場合は1本目の指は左手の親指です。その左側には指がないので十の位は0、右側の指は9本なので一の位は9、よって9×1＝09となります。

 

9×10の場合は10本目の指は右手の親指です。その左側の指は9本なので十の位は9、右側には指がないので一の位は0、よって9×10＝90となります。

 

九の段を順に書き出してみると、答え（積）にルールが見つかります。一の位は9、8、7、6、5、4、3、2、1と小さくなり、逆に十の位は0、1、2、3、4、5、6、7、8、9と大きくなります。

 

そして十の位と一の位の和は9です。両手合わせて10本の指のうち1本の指を折れば、残りは9本です。左の親指から順に折ることで答えの十の位が折った指の左側に、一の位が右側に現れるようになります。

 

 

両手を使う計算術その2　かけ算九九　5以上同士のかけ算

 

 

九の段以外にかけ算九九を両手で計算する方法があります。9×8を例に説明してみます。

 

計算術その1と同じように、まず手の裏を自分にみせて両手をそろえます。左手が9、右手が8を表すようにします。それぞれ10との差だけ指を折ります。左手は10－9＝1（本）、右手は10－8＝2（本）です。これで準備OKです。

 

立っている指の合計を数えると左手が4本、右手が3本なので4+3＝7（本）です。これが答えの十の位になります。最後に折った指の数同士の積を計算します。

 

左手、右手それぞれ1本、2本なので1×2＝2です。これが答えの一の位になります。9×8＝72というわけです。

 

6×7ならば、左手は10－6＝4（本）の指を折り、右手は10－7＝3（本）の指を折ります。

 

立っている指同士の和は1+2＝3、折っている指同士の積は4×3＝12となるので、答えの十の位は3に12の十の位1を足した4、一の位は12の一の位2となり6×7＝42となります。

 

この計算術は、折った指同士の積の計算、すなわち5以下同士のかけ算九九がわかっていれば、5以上同士のかけ算九九が計算できるというものです。

 

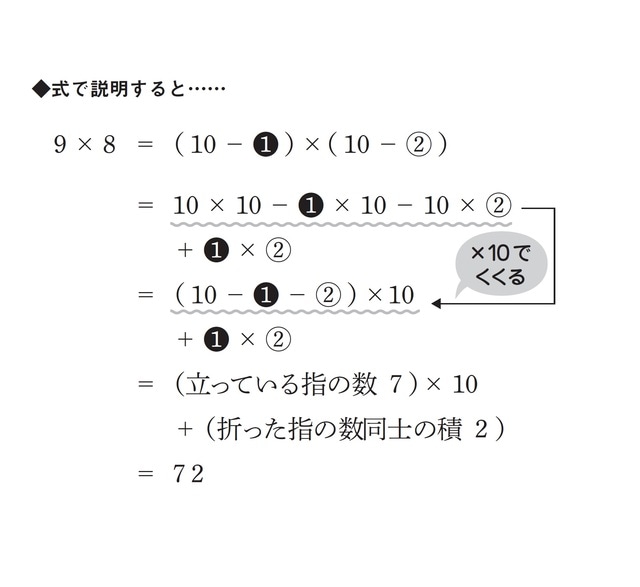
これを式で説明してみると下図のようになります。9と8をそれぞれ10－1、10－2と表してかけ算することで1と2（折った指の数）を使った計算に変換しています。

 

100に近い数同士のかけ算はむしろ“より楽”に

両手を使う計算術その3　100に近い数同士のかけ算　98×97

計算術その2は大きな数に応用することができます。100に近い数同士のかけ算は、100との差を利用することで楽に答えを求めることができます。

 

98×97を例に説明してみます。

 

 

99×99ならば、（ステップ1）100との差は1と1。（ステップ2）1＋1＝2を100から引いて98。（ステップ3）1×1＝1より下2桁は01。（ステップ4）98と01をあわせて9801が答え。

 

 

一見大きな数同士のかけ算は面倒に思えますが、100との差が小さい数になるので逆に計算が楽になるのが面白いところです。

 

 

桜井 進

株式会社sakurAi Science Factory　代表取締役