懐かしい法則で頭の体操
「相似則」と「指数法則」―─。学校で勉強したこの二つの法則を、なんとなく覚えている人も多いと思います。この二つの法則を使った数学クイズに挑戦してみましょう。
「相似則」とは、「面積は長さの二乗に、体積は長さの三乗に比例する」という法則です。
「指数法則」とは、指数のかけ算は足し算として、割り算は引き算として計算できる、なんとも便利な法則です。
Q.それでは、「相似則」のクイズです。
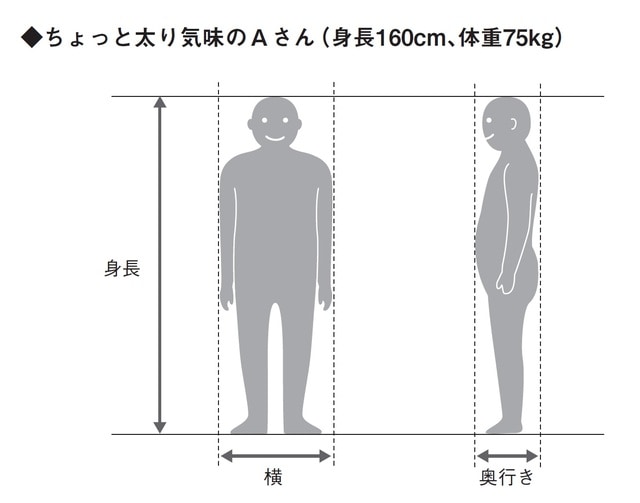
会社の健康診断で太りすぎを注意されたAさん(身長一六〇センチ、体重七五キログラム)。Aさんは、同僚Bさんの中肉中背の体型(身長一七五センチ、体重七〇キログラム)を見習いたいと思い、Bさんのような体型を目指すことにしました。Aさんは目標体重を何キログラムに設定すればいいのでしょうか。
ポイント
▼体型と筋肉質が似ている相手を選び、「相似則」を利用する!
▼身長の比=長さの比
▼体積比は、長さの比(相似比)の三乗
計算方法はシンプル
計算方法はいたってシンプルです。しかし、その計算を意味あるものにするためには準備が必要です。まず、ちょっと太り気味のAさんが探さなければならないのは「理想とする人」です。
身体のバランスは複雑です。顔の大きさ、肩幅、腕の長さ、身長に対する脚の長さの比……など、たくさんのポイントがあります。ですから、Aさんは体重を減らしたときの体型に近いと想像される体型の持ち主を選ぶことが大切です。
そこで、同じような体型の二人を比較するためには身長比を調べます。つまり、体型が似ている二人とは、「身長比=横の比=奥行きの比」となると考えるわけです。
そして、体型の他にもう一つ、計算の前提になることがあります。それは、体重と体積の比(身体密度)です。
人間の場合、比重は体脂肪よりも筋肉のほうが大きいのです。つまり、筋肉質の人はそうでない人より身体密度が大きい。その意味で、やはりAさんは筋肉の付き具合もだいたい同じような人を目標とすることになります。
以上、「体型」と「筋肉質の具合」の二つの点に注意して理想の人を見つけてはじめて相似比から体重比、すなわち体重比の計算が意味をもつことになります。
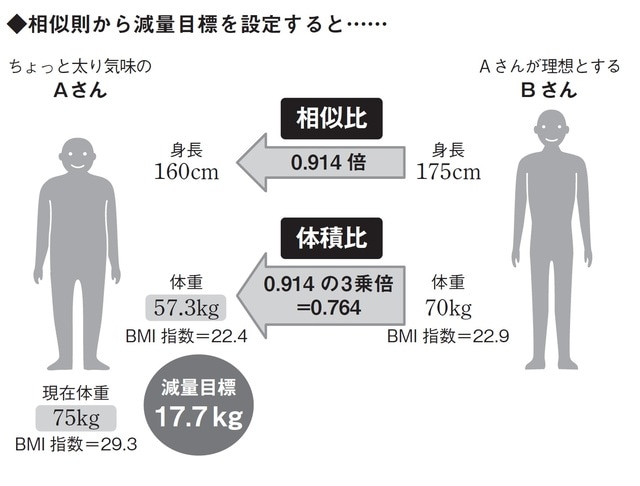
Aさんが理想とするBさんの体型は、身長一七五センチ、体重七〇キログラムでした。まず、身長から長さの比(相似比)を求めると、一六〇÷一七五=約〇・九一四となります。するとその三乗が体積比(=体重比)となります。
計算すると〇・九一四の三乗は、〇・九一四×〇・九一四×〇・九一四=約〇・七六四となりますね。
したがって、身長一六〇センチのAさんが、身長一七五センチのBさんと体型が相似になる体重は、七五キログラム×〇・七六四=五七・三キログラムとわかります。
この計算で求めたAさんの理想体重が、本当にBさんの体型と相似なのかどうかを確認してみましょう。
それには、肥満度の指数であるBMI指数(ボティマス指数)を使います。BMI指数は、体重を身長(メートル)の二乗で割って求めることができます。あわせて計算してみましょう。
理想の体型とするBさんのBMI指数は、七〇÷(一・七五×一・七五)=約二二・九。それに対して、ダイエット前のAさんのBMI指数は、七五÷(一・六×一・六)=約二九・三。
理想とするBさんと相似になる五七・三キログラムに減量したときには、五七・三÷(一・六×一・六)=約二二・四となります。たしかに理想とするBさんのBMI指数に近い値になっていることが確かめられます。
ダイエットはつい「体重」だけに目が行ってしまいますが、身長という「長さの比」や「身体密度」という筋肉の付き具合に注目してこそ、バランスのとれた健康的な体型になれるのですね。
そして、そのお手伝いをするのが「相似則」という数学の法則なのです。
桜井 進
株式会社sakurAi Science Factory 代表取締役