サルが見せた驚くべき損得計算能力
「十分に合理的に見えるサルたちでさえ、たまには損得計算を間違えたりして非合理的な行動を取ってしまわないか?」
研究者たちはこの問いの答えを出すため、次のように自販機の設定を変えて実験していきました。一緒に考えてみてください。
-------------------------------------
【実験1】もらったおこづかいを1枚使って、好きな自販機から買ってください。
自販機A…リンゴが1つ置いてあり、トークンを入れると必ず1個が出てくる
自販機B…リンゴが2つ置いてあり、トークンを入れると50%の確率で2個出てくるが、50%の確率で1個しか出てこない
-------------------------------------
サルたちの多くは自販機Bのほうを好みました。やはりサルたちは損得計算ができているようです。リンゴがもらえると期待できる個数(期待値)は、自販機Aで1個、自販機Bで1.5個ですから。
評価していただきたいのは、言葉で伝えられないので、サルたちはこの自販機の仕組みを体験的に理解して、その情報を次の買い物のときに使いこなしていた、ということです。
しかし、「マイナスを極端に嫌う」と計算が狂う
では、もうひとつ考えてみましょう。
-------------------------------------
【実験2】もらったおこづかいを1枚使って、好きな自販機から買ってください。
自販機C…リンゴが1つ置いてあり、トークンを入れると50%の確率で1個出てきて、もう50%の確率でオマケが付いて2個出てくる
自販機D…リンゴが2つ置いてあり、トークンを入れると50%の確率で2個出てきて、50%の確率で1個しか出てこない
-------------------------------------
さて、サルたちのお好みは、自販機Cだそうです。研究者たちの言葉を借りれば、「興味深いことにサルたちはまるで人間の実験参加者かのように振る舞った」らしいのですが、みなさんはいかがだったでしょうか。
「ちょっと待って、自販機Cと自販機Dの違いがわからない!」という人もいるかもしれません。
損得計算できるサルなら「もらえるリンゴの期待値は1.5個で変わらないので、自販機Cでも自販機Dでもどちらでもいい」と考えてもいいはずです。
でも、サルたちの反応は違いました。結果が変わらないのに選択が偏(かたよ)るというのは、あまり論理的ではないように思えます。
では、なぜ選択を変えるのでしょうか。考えられるひとつの仮説は、サルの心の中では同じ1個のリンゴでも、減って出てくるのはどうしても嫌だと評価しているということです。
オマケの1個がもたらすうれしさより、損失に見える1個がもたらす悲しみが上回る。何かを失うことを極端に嫌がる「損失回避」の強い感情が表れたのだ、と考えられるわけです。
いつでも、どこでも、合理的に選択肢を選んでいる合理的経済人は期待値が同じなのでどちらでもいいと判断しますが、サルは見た目の損失を回避したいがために偏った非合理的な判断をしてしまうのです。
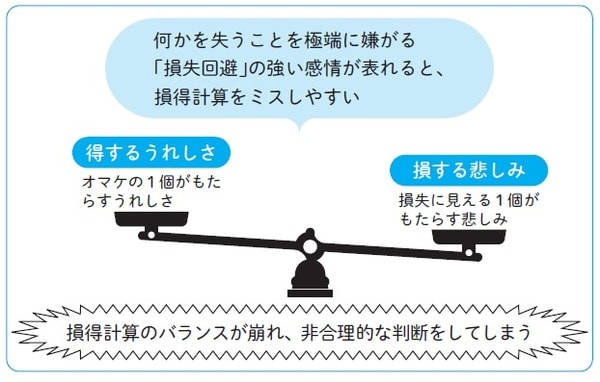
【図表】損得計算のバランスが崩れ、非合理的な判断をしてしまう 出所:太宰北斗著『行動経済学ってそういうことだったのか! -世界一やさしい「使える経済学」5つの授業-』(ワニブックス)より
伝統経済学では「人はいつでも合理的」と仮定するが…
サルたちが「50%の確率で」という状況を突きつけられたように、私たちも多くの選択を「どっちが起きるかわからない、不確実なシチュエーション」で迫られます。
価格が下がるかもしれない株を買うべきか、1着になるかどうかわからない競走馬の馬券を買うべきか──。
経済学では一般的に、ある出来事が起こりえるときの不確実さのことを「リスク」と呼びます。
甘い物をもらえるかもらえないか、もらえるとすれば何個もらえるのか。悪いことでも良いことでも、起こりえる出来事が不確実であれば、なんでもリスクです。
買った株式の価格が予想外に上がってしまいかねないのもリスクなら、流れで買っただけの馬券が当たってしまいかねないのもリスクです。
さて、先ほどの、サルたちの非合理性の話を思い返してください。もともとは結構まともに損得計算していましたよね。賢かったサルたちは、リスクのあるギャンブルの損得計算を期待値で計算してなかったわけですが、みなさんはどうでしょうか。1問、考えてみてください。
-------------------------------------
【質問】次の2つの選択肢のうち、あなたの好きなほうを選んでください。
A…85%の確率で10億円がもらえ、15%の確率で何ももらえない
B…100%の確率で8億円がもらえる
-------------------------------------
この手の質問をすると多数派の人はBを選びます。多くの人は、なぜ、Bを選ぶのでしょうか?
期待値を計算するとAの選択は、8.5億円となります。これはBの期待値である8億円よりも高くなっていて、Aのほうが5000万円もお得だと言えます。“損得”はどこへいってしまったのでしょう。それでも、Bを選ぶ理由はもちろん「15%の確率で何ももらえない危険を避けたかったから」ですよね。
不確実な状況では“心の満足度が高そうな選択肢”を選ぶ
ここで、少しだけ伝統的な経済学における議論を整理しておきます。
行動原理を考えるとき、伝統経済学では「人は心の満足感の最大化を図るはずだ」と考えます。この心の満足感のことを効用と呼びます。
どちらが起こるかわからない不確実な状況下では、この効用の期待値を計算して選択の指標としていると考えれば、あなたがBを選んだ理由を説明できます。
つまり、不確実な状況では、できるだけ心の満足度が高いと期待できる選択肢を選んだと考えればいいわけです。
たとえばあなたにとって、資産10億円であることの効用が100点で、資産8億円であることの効用が90点だとします。
Bを選べば効用はそのまま90点ですが、Aを選ぶと100×0.85=85点となります。これなら、Bを選ぶべきですよね。
つまり、伝統的な経済学では、「リスクを取るか取らないかも、個人の価値観次第だと考えればいい」としたのです。
しっかりと損得を計算したいとき、必要になる「視点」
伝統的な経済学におけるこのアイデアは「期待効用理論」と名付けられています。多くの場合で基本とされるポイントは2つ。
●心の満足度(効用)は、資産額などの「変化」ではなく「水準」で決まる
●リスクが好きか嫌いか、その好みは「水準」に応じて一貫している
最初のポイントの意味は単純で、資産が1億円あるのなら、資産が増えて1億円になっても、資産が減って1億円になっても、どちらのときでも満足度は一緒のはずだ、という意味です。0円+1億円=2億円-1億円、というわけです。1億円で買えるものに変わりはないから、態度も変わらないという風に考えるのです。
もうひとつのほうは、あなたがリスクをどのように回避したがるか追求したがるかは、資産状況に応じて既定されているということです。かいつまんで言うと、リスクについても「あなたの好みにいつでも従って」というイメージです。
合理的経済人なら、ここでも効用の期待値の計算をコンテクストなどには惑わされず、しっかりできていることになります。
もちろん、リスクがあるので残念なほうの結果になることもあるわけですが、わかる限りで確率なども計算に含めていたはずですから、基本的にはそうなることも織り込み済みだったと考えられます。
なんだかわかるようなわからないような話で、不思議に思う人もいるかもしれません。でも、次回以降のゴルフの記事で少し振り返りますので、とりあえず押さえておきましょう。
ついうっかり非合理的な判断をしないように損得をしっかり計算したいとき、意外と必要な視点となってきます。
太宰 北斗
名古屋商科大学 商学部 准教授
慶應義塾大学卒業後、消費財メーカー勤務を経て、一橋大学大学院商学研究科博士後期課程修了。一橋大学大学院商学研究科特任講師を経て現職。専門は行動ファイナンス、コーポレートガバナンス。
第3回アサヒビール最優秀論文賞受賞。論文「競馬とプロスペクト理論:微小確率の過大評価の実証分析」により行動経済学会より表彰を受ける。
競馬や宝くじ、スポーツなど身近なトピックを交えたり、行動経済学で使われる実験を利用した投資ゲームなどを行ない、多くの学生が関心を持って取り組めるように心がけた授業を行う。






























