平均と中央値

算術平均、幾何平均、調和平均の3つの平均で表しにくいものが「並」という概念です。「並」を表すのが「中央値」です。中央値はデータを大きさの順に並べた時に中央にくる数字で、中央値より大きな数字のデータ数と、中央値より小さな数字のデータ数が同じになります。

「並」という概念

これまで算術平均、幾何平均、調和平均、の3つの平均についてご説明してきましたが、これら3つの数字でも表しにくいものがあります。それが「並」という概念で、一般的に使われる「平均」という言葉がイメージさせる「並」は「平均」では表しにくいことがあります。

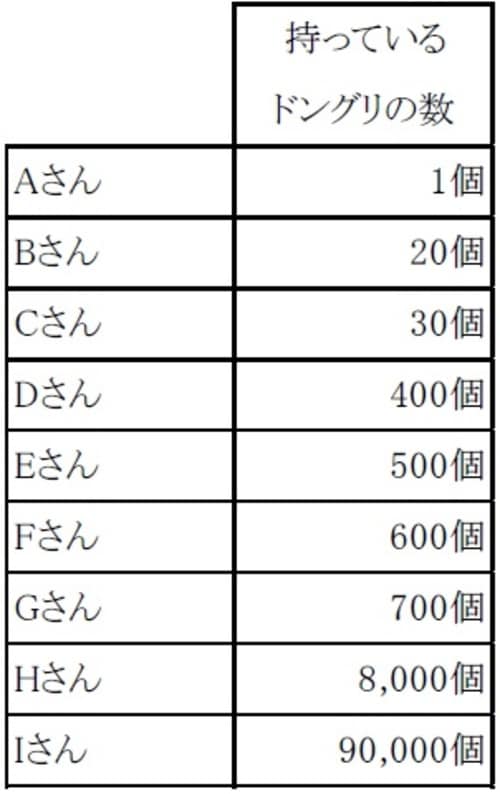
例えば、右の表のようにAさんからIさんの9人が持っているドングリの数に大きなバラつきがある場合、算術平均は以下の通りです。

（1+20+30+400+500+600+700+8,000+90,000）÷9＝11,139個

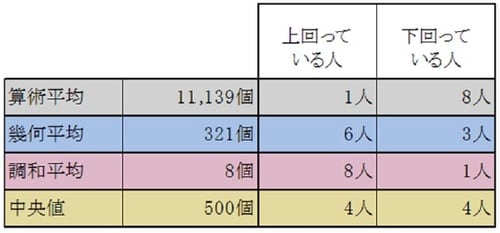
このように大きな数字の影響を強く受けて11,139個となります。この9人は「平均すると11,139個のドングリを持っています」と言っても、実際に11,139個を超えるドングリを持っているのは1人だけで、8人はこの数字に及ばず、7人の人は遠く及ばない数しか持っていません。

一方、幾何平均は、以下の通りです。

9√(1×20×30×400×500×600×700×8,000×90,000)＝321個

このように321個となりますが、今度は数字が小さすぎて9人中6人が上回っており、もしここに321個のドングリを持った人が現れても、この人が持っているドングリの数はこのグループの中で「並」とは言えません。

調和平均は以下のとおりです。

9÷（1/1+1/20+1/30+1/400+1/500+1/600+1/700+1/8,000+1/90,000) = 8個

幾何平均同様、数字が小さすぎてとても「並」とは言えません。

［図表1］算術平均、幾何平均、調和平均

「中央値」とは

この「並」をよく表してくれるのが「中央値」です。中央値はデータを大きさの順に並べた時に中央にくる数字で、データが偶数個の場合は中央2つの数字の算術平均です。つまり、中央値よりも大きな数字のデータ数と、中央値よりも小さな数字のデータ数が同じになるということです。5つのデータの中で3番目の数字、101個のデータの中の51番目の数字、というのは「平均」という言葉イメージさせる「並」をよく表してくれます。

［図表2］算術平均、幾何平均、調和平均、中央値

中央値：データを大きさの順に並べた時に中央にくる数字を確認しましょう。

例1：｛32、65、82、105、147｝の中央値は82

例2：｛32、65、82、105、147、205、310｝の中央値は105

例3：｛32、65、82、105、147、205、310、321、418｝の中央値は147

当レポートの閲覧に当たっては【ご注意】をご参照ください（見当たらない場合は関連記事『実践的基礎知識役に立つ平均編（4）＜平均と中央値＞』を参照）。

カメハメハ倶楽部セミナー・イベント

【4/16開催】相続人の頭を悩ませ続ける
「共有名義不動産」の出口は“売却”だけじゃない！
問題点と最新の解決策を藤宮浩氏が特別解説

【4/16開催】次世代のオルタナティブ投資
「プライベートクレジット投資」とは

【4/17開催】調査官は重加算税をかけたがる
相続税の「税務調査」の実態と対処方法

【4/19開催】良い案件を見つける3つの方策とは？
「日本型オペレーティングリース」投資の基礎講座

【4/20開催】「相続手続き」完全マスター講座
～相続人調査、財産調査、遺産分割協議～