実践的基礎知識役に立つ平均編（2）＜算術平均と幾何平均＞

調査官は重加算税をかけたがる
相続税の「税務調査」の実態と対処方法
＞＞4月2日（水）LIVE配信

算術平均と幾何平均

算術平均と幾何平均は、それぞれに特徴があってどちらが優れているということではなく、大切なことは両者の特徴を知り、意味するところを知ることです。算術平均とは一般的によく使われている平均で、対象となる全データを合計してデータの個数で割ることで求められます。また、幾何平均とは累積結果に至るまで平均してどのくらいのペースで変化していったのかを表すもので、平均収益率や平均成長率などを考える上で役に立ちます。

幾何平均

前回のレポートで、「幾何平均(相乗平均)」は平均収益率や平均成長率、平均変化率を考える上で役に立つと紹介させていただきましたが、一般的な算術平均(相加平均)とどう違うのでしょうか。

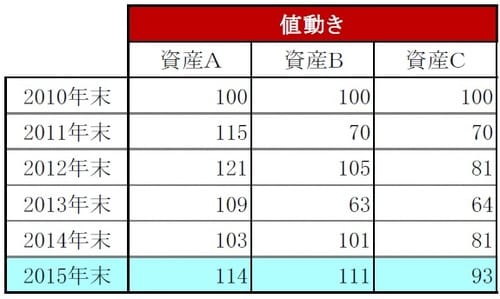
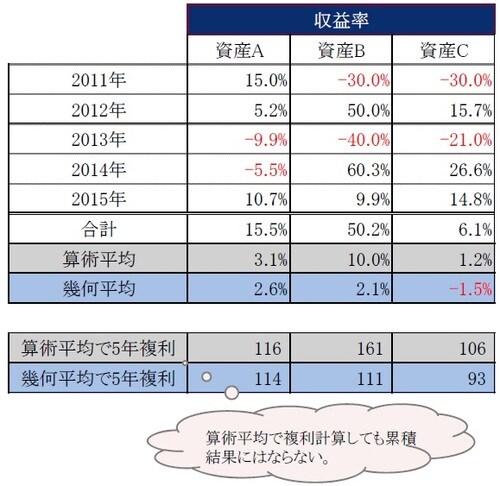
たとえば、図表1のような値動きをした資産A、B、Cがあったとします。各資産の各年の収益率を計算すると図表2のようになります(それぞれ図表1、2参照)。

［図表1］各資産の値動き

［図表2］各資産の収益率 ※数値は四捨五入して表示しているため、表示されている数値での計算結果と不一致となる場合があります。

資産Aの収益率の算術平均は

(15.0%+5.2%-9.9%-5.5%+10.7%)÷5=3.1%

と3.1%になります。

もし、この算術平均の3.1%で5年間複利運用をすると

100×(1+0.03)5=116

となり、100は116まで増えることになります。この116は2015年末の114という値と一致しません(図表2参照)。

一方、資産Aの収益率の幾何平均は

5√{(1+15%)×(1+5.2%)×(1-9.9%)×(1-5.5%)×(1+10.7%)}-1=2.6%

と2.6%になります。

この幾何平均の2.6%で5年間複利運用をすると

100×(1+0.026)5=114 

となり、2015年末の114と一致します。

実は、これはごく当たり前のことで、算術平均というのは相加平均という言葉が示すように、各数字を加算、つまり足して計算するため、算術平均を5回足し合わせれば各収益率の合計に一致しますが、複利計算をしても累積結果にはなりません。

幾何平均は相乗平均という言葉が示すように各数字を乗算、つまり掛けて計算するため、足しても各収益率の合計にはなりませんが、複利計算すれば累積結果と一致します。

このように、各年の平均収益率や平均成長率、平均変化率のような、「それまでの結果から何%変化したか」を集計したものを使って、累積結果に至るまでに平均してどのくらいのペースで変化していったのかを考えるうえで、幾何平均は役立ちます。

当レポートの閲覧に当たっては【ご注意】をご参照ください（見当たらない場合は関連記事『実践的基礎知識役に立つ平均編（2）＜算術平均と幾何平均＞』を参照）。

カメハメハ倶楽部セミナー・イベント

【4/10開催】
「豪州マリーナ投資」の魅力
レジャー/ツーリズムをテーマとした
“オルタナティブ不動産投資”とは

【4/10開催】
弁護士が解説する投資用物件の
「サブリース契約解除」実務対応

【4/15開催】
キャピタルゲインも期待できる環境に！
「債券投資」のタイミングと
具体的な取り組み方

【4/16開催】
その“貢献”は認められるのか？
相続権がない親族でも請求できる
「特別寄与料」とは

【4/16開催】
一級建築士、土地家屋調査士、
不動産鑑定士、相続専門税理士
４つの視点による「相続税土地評価」
と相続対策の進め方