正四面体の性質…頂点、辺、面の数は？

前回の記事（難関中学入試…大人も頭を抱える「正多面体は何種類？」の答え）で、正多面体は全部で5種類ということがわかりました。ここでは、それぞれの性質を確認していきましょう。

 

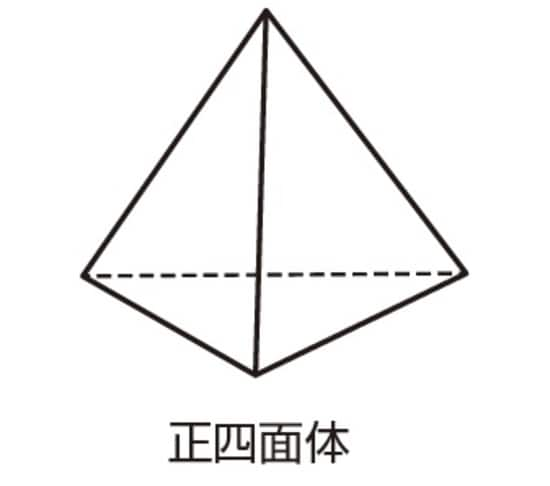
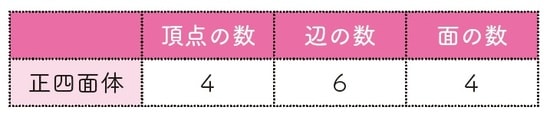
まずは、正四面体の頂点の数、辺の数、面の数を確認してみましょう。これは簡単に数えることができます。

 

立方体と正八面体の特別な関係

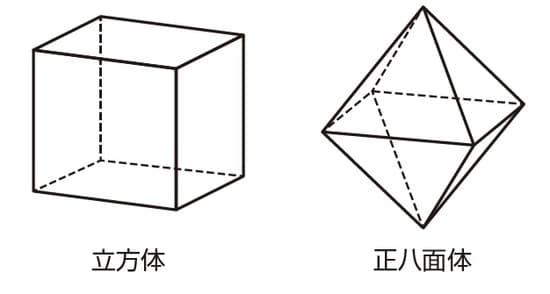
続いて、立方体と正八面体についても数えてみましょう。

 

立方体と正八面体の数字を比べて何か気づきませんか？　辺の数が同じで、頂点の数と面の数がちょうど入れ替わっていますね。これは偶然ではありません。立方体と正八面体には、特別な関係があります。そのため、頂点と面の数が入れ替わる関係になっているのです。

 

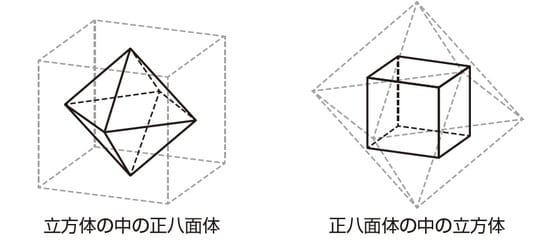
立方体の各面の真ん中を結ぶと正八面体ができ、正八面体の各面の真ん中を結ぶと立方体ができます。

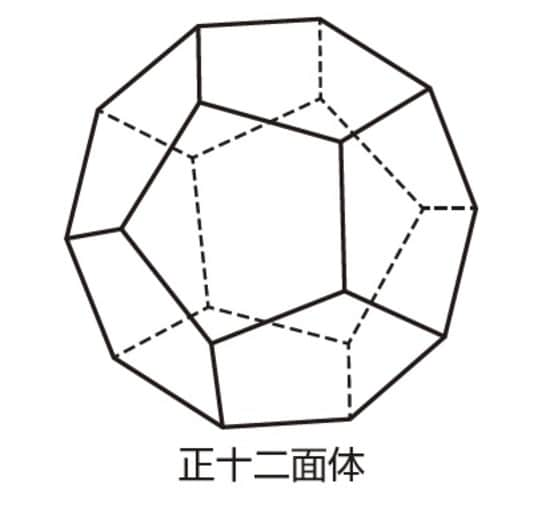
正十二面体の頂点・辺・面の数

正十二面体についても確認してみましょう。数が多くなってきたので、計算で求めてみます。

 

正十二面体なので、面の数が12枚なのはわかっています。すべての面をバラバラにして、組み立てていく様子をイメージしましょう。

 

正五角形が12枚あるので、バラバラにすると、

頂点の数は、5×12＝60個あり、

辺の数も、5×12＝60本あることになります。

 

ここで、バラバラの面を立体に組み立てていくと、３つの頂点が重なって正十二面体の１つの頂点になっていることがわかります。

 

よって、頂点の数は、60÷3＝20個と求められます。

 

また、2つの辺が重なって正十二面体の1つの辺になっていることがわかります。同様に、辺の数は、60÷2＝30本と求められます。

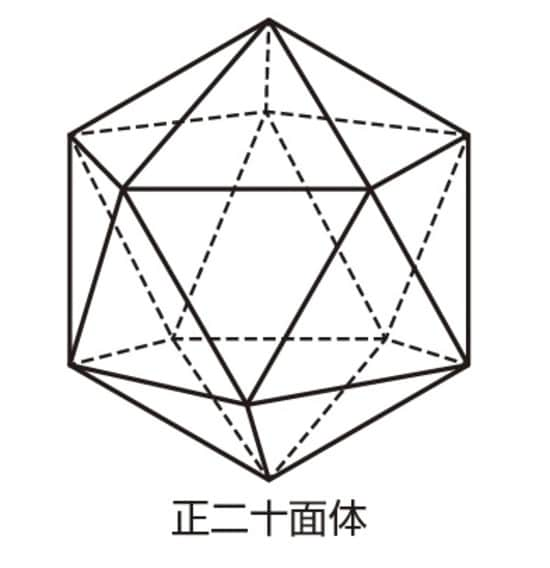
正二十面体の頂点・辺・面の数

正二十面体についても、同じように計算してみましょう。

 

5枚の正三角形が重なって、正二十面体の1つの頂点になっているので、頂点の数は、（3×20）÷5＝12個。

 

2本の辺が重なって、正二十面体の1つの辺になっているので、辺の数は、（3×20）÷2＝30本になります。

正十二面体と正二十面体の性質と関係性

わかってきましたか？　正十二面体と正二十面体について、まとめておきます。

 

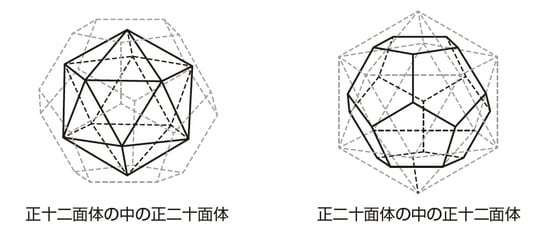
このようにまとめると、何か気づくことはありませんか？　立方体と正八面体の時と同じように、辺の数が同じで、頂点の数と面の数が入れ替わっています。

 

正十二面体と正二十面体の関係も、立方体と正八面体の関係と同じで、お互いに中にピッタリとはまるようになっているのです。

 

それぞれの性質や関係性がわかると、正多面体に興味がわいてきませんか？

 

 

松本 亘正
中学受験専門塾ジーニアス　代表

教誓 健司
中学受験専門塾ジーニアス　講師

 

【関連記事】

■税務調査官「出身はどちらですか？」の真意…税務調査で“やり手の調査官”が聞いてくる「3つの質問」【税理士が解説】

 

■月22万円もらえるはずが…65歳・元会社員夫婦「年金ルール」知らず、想定外の年金減額「何かの間違いでは？」

 

■「もはや無法地帯」2億円・港区の超高級タワマンで起きている異変…世帯年収2000万円の男性が〈豊洲タワマンからの転居〉を大後悔するワケ

 

■「NISAで1,300万円消えた…。」銀行員のアドバイスで、退職金運用を始めた“年金25万円の60代夫婦”…年金に上乗せでゆとりの老後のはずが、一転、破産危機【FPが解説】

 

■「銀行員の助言どおり、祖母から年100万円ずつ生前贈与を受けました」→税務調査官「これは贈与になりません」…否認されないための4つのポイント【税理士が解説】