検索
中学受験では、灘、開成、麻布といった超難関校ほど「図形」の単元が入試に多く出る傾向があります。この単元は、「わかる」と「正解する」のギャップが大きくなりやすいため、注意が必要です。難関校合格のために不可欠な単元の学習方法を紹介します。
教誓先生：読み方は「きょうせいせんせい」。名は体を表すのか、教えることが大好き。幼い頃から約数の多い数は「よい」数だと感じていたが、あまり共感を得られないらしい。出題者の意図をくんで解くことを心掛けている。
まなぶ君：算数は好きだけど、勉強は嫌いで、できればラクしたいと思っている小学5年生。6年生になったら中学受験をするので塾に通っている。たまにめんどくさがり屋の一面をのぞかせる。
教誓先生：まなぶ君、私はピザが好きでよく注文するんです。でも、同じ大きさに切るのが大変なんですよね。同じ大きさに4等分するにはどうしたらいいかわかりますか？
まなぶ君：先生、ピザが好きなんですね…。4等分するには、まず縦に切って、横に切ったら4つになりますよ。
教誓先生：いいですね。では、この紙をピザだと思ってやってみてください。
まなぶ君：あれ、大きさがそろわないなぁ…。
教誓先生：縦と横に切り分けるというのはとてもいいのですが、大きさを同じにするためにはもっと意識するポイントがあるんです。
まなぶ君：真ん中を通るようにとは思ったんだけど、うまくいかなかったなぁ。
教誓先生：では、もう一度この円に線を引いてみましょう。
まなぶ君：真ん中を通るように…う〜ん…うまく線を引く自信がないです。
教誓先生：では、次のことを意識してみてください。「このピザの中心がここかな」とわかったら、そこを通ることだけを考えてまっすぐに線を引いてみてください。
まなぶ君：わかりました。中心をとにかく見て…できた！
教誓先生：次は横ですね。これも中心を通ることだけを考えてみましょう。
まなぶ君：あっ、今度はうまく4つに分けられました。ほとんど同じ形です。ポイントは中心ということなのか！
教誓先生：そうです。「円の命は中心」です。そもそも円は中心があるから存在するのです。
まなぶ君：じゃあ、円の問題で補助線を引く時には、中心を意識するといいのかな。
教誓先生：その通り！ 絶対ではありませんが、そういう考え方を知っておくことは重要ですよ。補助線というのは、ただ引けばよいというものではありません。手を動かして考えることは大事ですが、むやみやたらに引いて、ぐちゃぐちゃになってしまうのもよくありません。
人生と同じです。だいたい、答えが見えないような世の中で、公式をあてはめたらいいなんてことはないのです。どうやってシンプルに美しく…。
まなぶ君：ふぁ〜あ。ピザのことを考えていたら、なんだかお腹がすいてきちゃった…。
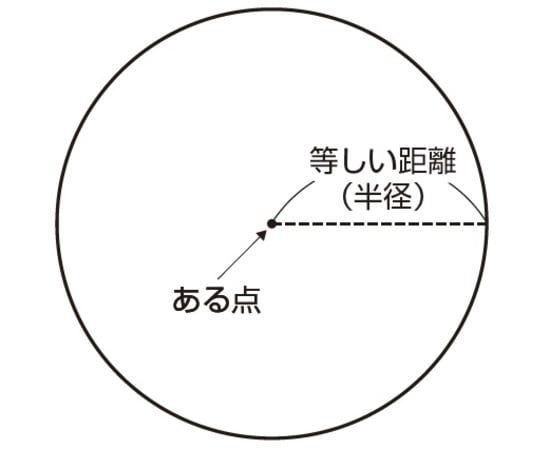
円は、ある点から等しい距離にある点の集合
円の問題を解く時にもっとも大切なことは、適切な補助線を引けるようになることです。そして、それは簡単にできます。
まず、円とはどんな図形か説明できるようになりましょう。「円って何？」って言われると、なかなか説明しづらいのではないでしょうか。
「丸」や「真ん丸」といった単語だけでは、どんな図形かを説明したことになりません。コンパスを使って円を描く様子をイメージしてみるとよいでしょう。
円とは、「ある点から等しい距離にある点の集合」のことです。「ある点」のことを円の「中心」と言い、「等しい距離」のことを円の「半径」と言います。
半径が等しいということは、円やおうぎ形の問題を考えていくうえでとても大切な要素となります。半径が等しいなんて当たり前と思うかもしれませんが、難しい問題ほど、大事になってきます。
円周率は「円周が直径の何倍なのか」を表したもの
続いて、円周率について確認しておきましょう。
中学入試では円周率が「3.14」とだけ教えられることが多いのですが、厳密に言えば、「円周率＝3.14」ではありません。本来の言葉の意味をしっかりと理解しておくことは大切です。
円周率を計算すると、「3.14159265358979…」とどこまでも続いていきます。よく算数好きな子が「円周率をずっと言える！」と自慢したりしますよね。
この数の小数第三位を四捨五入して、およその数にしたものが「3.14」なのです。問題によって、円周率が「3」や「3.1」や「22/7」となることもあるので、注意して問題文を読む必要があります。
ちなみに中学校では小数ではなく「π（パイ）」という記号で表します。3.14を使って計算すると、計算の桁（けた）数が多くなりがちなので、中学校のほうがラクに思えるかもしれませんね。
ちなみに、πはアップルパイなどのPIE（パイ）と発音が同じです。そして3.14。何か共通点に気づきませんか？
3.14を裏返してみると…PIE に見えてきますよね。アップルパイも丸い形をしていますよね。π、3.14、PIE。意外な共通点があると思いませんか。
円周率（3.14）のかけ算を覚えておこう
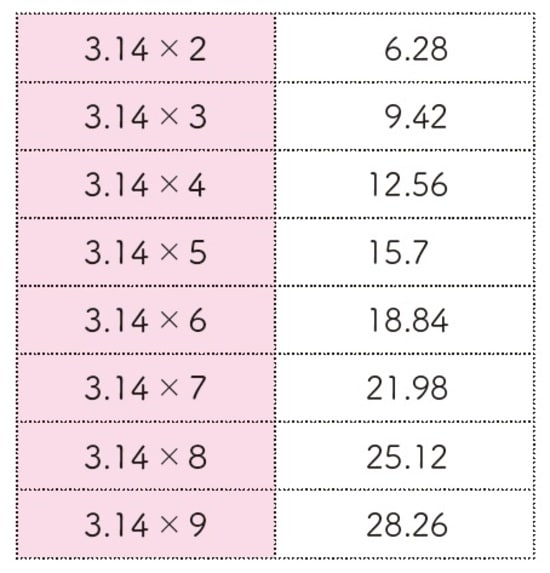
3.14を使った計算は、頻繁（ひんぱん）に出題されます。1桁（けた）の数とのかけ算を九九と同じように覚えておくと、大きな数と3.14をかけ算する時にも便利です。
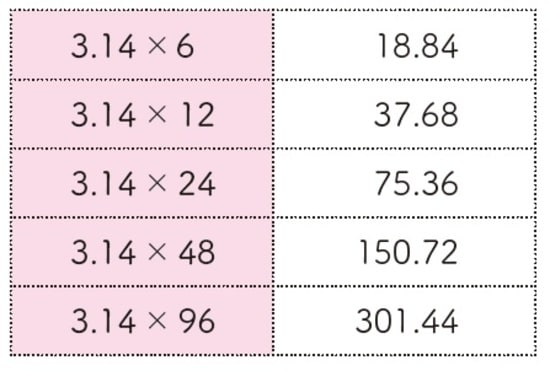
2桁（けた）の数についても、2倍ごとに整理して覚えておくとよいでしょう。3.14×6＝18.84を2倍ずつ増やしていくと次のようになります。
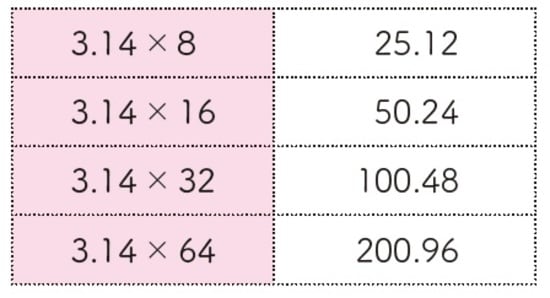
また、3.14×8＝25.12を2倍ずつ増やしたものは、以下の通りです。これらもよく登場します。
これらをすぐ答えられるようになれば、計算がかなりラクになり、計算ミスにも気づきやすくなります。「こんなものを覚えるのは邪道（じゃどう）だ。きちんと計算すればいい」という人もいるかもしれません。
でも、限られた時間でどれだけ正解できるかが問われる中学受験では、重要な数字を覚えておくことも大切です。何度も自力で計算したうえで、答えを頭に入れておいてくださいね。
松本 亘正
中学受験専門塾ジーニアス 代表
教誓 健司
中学受験専門塾ジーニアス 講師
【関連記事】
■税務調査官「出身はどちらですか？」の真意…税務調査で“やり手の調査官”が聞いてくる「3つの質問」【税理士が解説】
■月22万円もらえるはずが…65歳・元会社員夫婦「年金ルール」知らず、想定外の年金減額「何かの間違いでは？」
■「もはや無法地帯」2億円・港区の超高級タワマンで起きている異変…世帯年収2000万円の男性が〈豊洲タワマンからの転居〉を大後悔するワケ
■「NISAで1,300万円消えた…。」銀行員のアドバイスで、退職金運用を始めた“年金25万円の60代夫婦”…年金に上乗せでゆとりの老後のはずが、一転、破産危機【FPが解説】
■「銀行員の助言どおり、祖母から年100万円ずつ生前贈与を受けました」→税務調査官「これは贈与になりません」…否認されないための4つのポイント【税理士が解説】
