検索
【登場人物】
教誓先生：読み方は「きょうせいせんせい」。名は体を表すのか、教えることが大好き。幼い頃から約数の多い数は「よい」数だと感じていたが、あまり共感を得られないらしい。出題者の意図をくんで解くことを心掛けている。
まなぶ君：算数は好きだけど、勉強は嫌いで、できればラクしたいと思っている小学5年生。6年生になったら中学受験をするので塾に通っている。たまにめんどくさがり屋の一面をのぞかせる。
教誓先生：今日の授業では、サッカーボールを使います。
まなぶ君：えっ!? 体育の授業ですか？ やったー！
教誓先生：サッカーボールを見てください。この形から何か気づくことはありますか？
まなぶ君：あれっ!? よく見ると、サッカーボールって球体ではないんだ！ 球に似ているけど、ちょっと違うなぁ。
教誓先生：そうですね。もっと具体的に答えてみてください。
まなぶ君：正六角形と正五角形があります。それを組み合わせているのかな。
教誓先生：その通り！ 身近なものにも算数が隠れているんです。
まなぶ君：な〜んだ…。やっぱり算数の授業なのかぁ…。
教誓先生：さて、どうしてこういう形になっているのでしょうか？
まなぶ君：球体に近いけど、球体じゃない…。ん〜難しいなぁ…。球体のほうがいいと思うんだけどなぁ…。
教誓先生：そうですね。ただ、昔は革をつないでつくっていたので、きれいな球体にするのが難しかったのでしょう。そこで、同じ形を組み合わせることで球体に近いものを考えたのです。
まなぶ君：へぇ〜。でも、どうして同じ形にしなかったんだろう。正六角形と正五角形と組み合わせずに、同じ形でつくればよかったのに。
教誓先生：それはとてもいい疑問です。重要なのは、疑問を持ち続けること。今日は、美しい多面体の勉強をするのですが、同じ形でできた立体と言えば、何を思いつきますか？
まなぶ君：まず立方体かな。それから、正四面体。正三角形4枚でつくられるものですよね。
教誓先生：そうです。いいですね。でも、それではサッカーボールになりません。立方体を蹴けっていたらサッカーになりませんよね。
まなぶ君：ん〜そうだ！ 正八面体があった！
教誓先生：はい、また1つ思いつきましたね。でも、正八面体を蹴（け）るサッカーをイメージできますか？
まなぶ君：う〜ん…。じゃあ正百面体！ それならサッカーもできそうです！
教誓先生：まなぶ君…。果たして、そんな立体はつくれますかね…。では、勉強を始めていきましょう。
正多面体はたったの5種類しかない!?
正多面体は、次の2つの条件を満たす、へこみのない立体のことを言います。
条件①すべての面が等しい正多角形でできている
条件②すべての頂点に集まる面の数が等しい
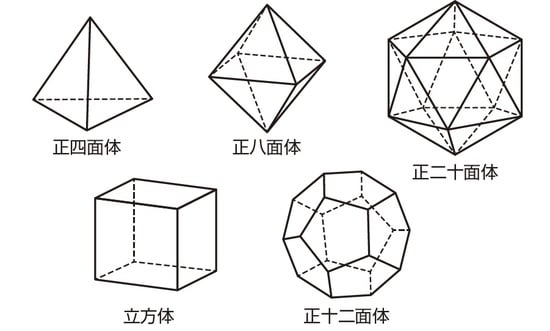
上の2つの条件を満たす図形は、全部で5種類あります。
これまでに登場した正四面体、立方体、正八面体の3種類に加え、正十二面体、正二十面体の2種類です。
正四面体、正八面体、正二十面体は各面が正三角形で、立方体は正方形で、正十二面体は正五角形でできていますね。
正多面体が5種類しかないことは、意外かもしれませんね。でも、面の形で分類すると簡単に説明できるのです。
正三角形の枚数を6枚にしてみると…
まずは、正三角形でできた正多面体を考えます。
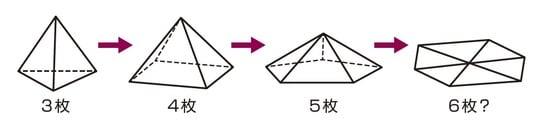
正三角形を集めて立体の頂点をつくることを想像してください。正三角形を3枚集めると、とがった頂点をつくれますよね。そして、正三角形の枚数を4枚、5枚と増やしていくと、少しずつなだらかな頂点へと変化していきます。
では、正三角形を6枚にしたらどうでしょう？
そうですね。平面になってしまい、頂点をつくることはできません。正三角形の1つの内角の大きさである60°が6つ集まると、60×6＝360°になります。
「正三角形は平面を敷（し）き詰（つ）めることができる図形だ」ということは基本ですが、平面になるということは、頂点をつくることができないということなのです。
正三角を使った正多面体は3種類だけ
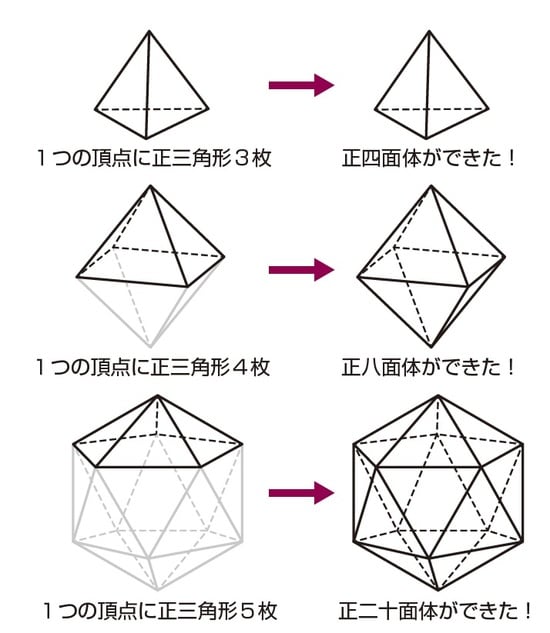
正三角形を1つの頂点に3枚集めると正四面体、4枚集めると正八面体、5枚集めると正二十面体ができます。
これで、正三角形を使った正多面体はこの3種類しかないことがわかりました。
正方形からできる多角形は立方体の1種類
正三角形以外の正多角形についても確認しましょう。
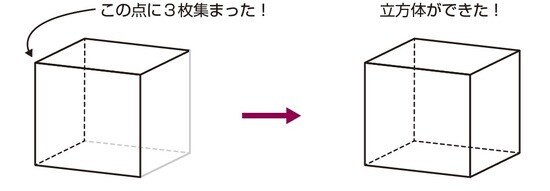
正方形は1つの内角の大きさが90°です。正方形3枚なら、90×3＝ 270°となり、360°より小さいので立体の頂点をつくることができます。
正方形4枚では、90×4＝360°となり、立体の頂点をつくれません。
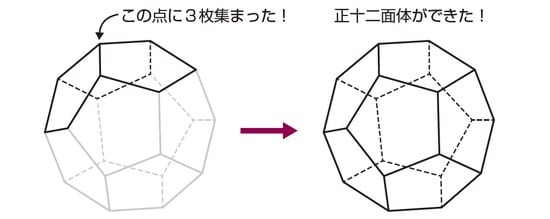
正五角形からできる多角形は正十二面体の1種類
正五角形は、1つの内角の大きさが108°です。正方形と同じように、3枚なら108×3＝324°で頂点をつくることができます。
正五角形4枚の場合、108×4＝432°となり、360°を超えてしまうので、立体の頂点をつくれません。
最後に、正五角形より頂点の多い正多角形についても確認しておきましょう。
正六角形は1つの内角の大きさが120°です。3枚なら120×3＝360°となり、頂点をつくることはできません。正七角形、正八角形、正九角形と形を変えたところで、1つの内角の大きさはどんどん大きくなって、頂点をつくれなくなってしまいます。
これで、正多面体が5種類しかないことがわかりましたね。
松本 亘正
中学受験専門塾ジーニアス 代表
教誓 健司
中学受験専門塾ジーニアス 講師
【関連記事】
■税務調査官「出身はどちらですか？」の真意…税務調査で“やり手の調査官”が聞いてくる「3つの質問」【税理士が解説】
■月22万円もらえるはずが…65歳・元会社員夫婦「年金ルール」知らず、想定外の年金減額「何かの間違いでは？」
■「もはや無法地帯」2億円・港区の超高級タワマンで起きている異変…世帯年収2000万円の男性が〈豊洲タワマンからの転居〉を大後悔するワケ
■「NISAで1,300万円消えた…。」銀行員のアドバイスで、退職金運用を始めた“年金25万円の60代夫婦”…年金に上乗せでゆとりの老後のはずが、一転、破産危機【FPが解説】
■「銀行員の助言どおり、祖母から年100万円ずつ生前贈与を受けました」→税務調査官「これは贈与になりません」…否認されないための4つのポイント【税理士が解説】
