検索
「円の面積＝半径×半径×3.14」の理由は？
円周率の意味がわかれば、円周の長さが「直径×円周率」で求められることはすぐわかります。ここでは円周率を3.14とします。
では、円の面積はどうやって求めればよいのでしょう？
もちろん、公式を覚えて実際に計算できることも必要ですが、それ以上に、どうしてその公式で面積が求められるかを説明できることが重要なのです。
面積は、1辺の長さが1の正方形の面積を1とした時に、その何倍なのかと考えて計算します。とは言え、円には曲線があるので、正方形と比べるのは難しそうに見えますね。そこで、円のままではうまく計算できないので、求めることができる図形になるよう、形を変える必要があります。
円を小さく切り分けて、長方形にして求める
形の変え方はいろいろとあるのですが、ここでは代表的な2つを紹介します。
上の図のように形を変えると長方形をつくることができます。円を小さく切り分けたおうぎ形を交互（こうご）に入れていくようなイメージです。
こう展開すると、長方形の縦の長さは円の「半径」です。そして、長方形の横の長さは「円周の半分」になっています。なぜ半分かと言うと、交互（こうご）に並べているからです。
つまり、「半径×円周の半分」を計算すると、面積を求めることができます。
円を小さく切り分けて、三角形にして求める
もう1つの方法がこちらです。
「前の図のことも、まだよくわからない…」という場合には、この説明は飛ばしても大丈夫です。
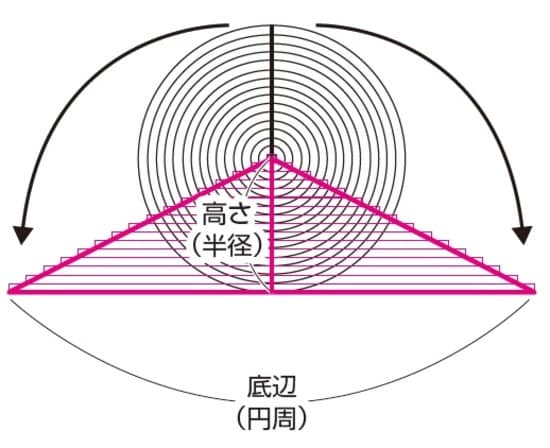
上の図のように形を変えると三角形をつくることができます。三角形の底辺が「円周」です。
そして、三角形の高さが「半径」になっています。つまり、三角形の面積の公式「底辺×高さ÷2」にあてはめて、「円周×半径÷2」の計算をすると円の面積が求められます。
補助線を用いて、円の中心を正しく見つけよう
ここまでの説明をふまえ、補助線の話に入っていきましょう。
次の問題を見てください。
図のように直径が12㎝の半円があります。色のついた部分の面積を求めなさい（※円周率は3.14とする）。
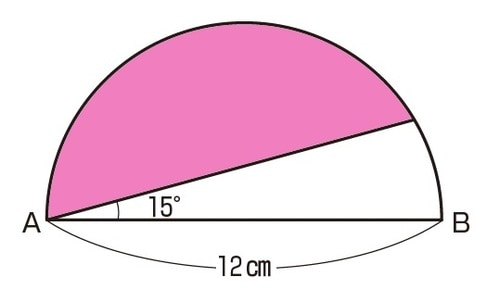
これは、毎年のように中学入試で出題される問題です。円やおうぎ形のことを正しく理解できているか確認できる良問と言えます。2020年にはフェリス女学院でも同じような問題が出題されていました。
このような問題形式で出題されるのがもっとも間違いやすいのです。
少し計算が大変かもしれませんが、続きを読む前に自分で一度答えを出してみてください。ここまで学んだ内容で解くことができる問題です。
まずは、よくある間違いを紹介してみましょう。
どこが間違っているかわかりましたか？
全体の面積から白い部分の面積を引くという発想で解くことはできます。半円の面積が56.52㎠というのは正しいのですが、白い部分の面積は18.84㎠ではありません。
白い部分が「半径12㎝、中心角15°のおうぎ形」というとらえ方が間違っているのです。
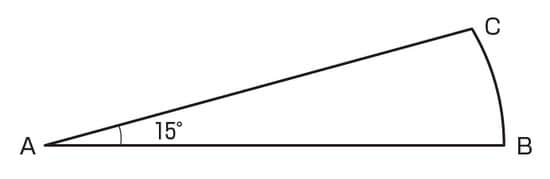
それでは、問題の白い部分に注目してみましょう。
この図形はおうぎ形ではありません。なぜなら、この図形の弧（こ）BCの中心はAではないからです。
円の中心の点を求めて、三角定規を見つける
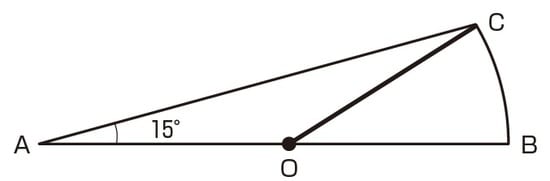
では、弧（こ）BCの中心はどこでしょう。それは全体の半円の中心と同じ場所です。つまり、辺ABの真ん中の点（O）です。その中心とCを結ぶ線を引くと次のようになります。
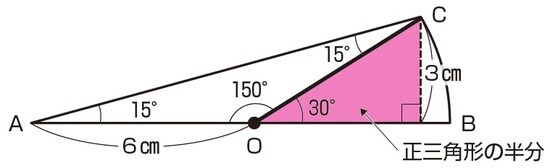
このように、白い部分は三角形とおうぎ形を組み合わせた図形だったのです。半径が等しいことから、三角形OACはただの三角形ではなく二等辺三角形であることもわかります。角度や長さを書き込んでおきましょう。
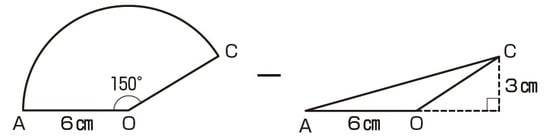
150°の外角が30°なので、正三角形の半分の形が隠れています。OA＝OC＝6cmより、OAを底辺とした時の高さは、30°・60°・90°の直角三角形の長さの比が2：1であることから、3cmになります。
これで、中心角が150°のおうぎ形OACから三角形OACの面積を引いて、答えを求めることができます。
おうぎ形OACの面積は、6×6×3.14×150/360＝47.1㎠
三角形OACの面積は6×3÷2＝9㎠
求める面積は、47.1－9＝38.1㎠
円の学習総まとめ
•円周率とは、円周の長さが直径の長さの何倍かを表したもので、3.14159265358979…とどこまでも続く小数になる。円周率の小数第三位を四捨五入すると3.14になる
•円周の長さは、直径×円周率（3.14）
•円の面積は、半径×半径×円周率（3.14）。もしくは、円周の長さ×半径÷2
•円やおうぎ形の問題では、中心と結ぶように補助線を引くことが大切
松本 亘正
中学受験専門塾ジーニアス 代表
教誓 健司
中学受験専門塾ジーニアス 講師
【関連記事】
■税務調査官「出身はどちらですか？」の真意…税務調査で“やり手の調査官”が聞いてくる「3つの質問」【税理士が解説】
■月22万円もらえるはずが…65歳・元会社員夫婦「年金ルール」知らず、想定外の年金減額「何かの間違いでは？」
■「もはや無法地帯」2億円・港区の超高級タワマンで起きている異変…世帯年収2000万円の男性が〈豊洲タワマンからの転居〉を大後悔するワケ
■「NISAで1,300万円消えた…。」銀行員のアドバイスで、退職金運用を始めた“年金25万円の60代夫婦”…年金に上乗せでゆとりの老後のはずが、一転、破産危機【FPが解説】
■「銀行員の助言どおり、祖母から年100万円ずつ生前贈与を受けました」→税務調査官「これは贈与になりません」…否認されないための4つのポイント【税理士が解説】
