「なぜ?」「どうして?」を投げ出さずに考えられる
前回の続きです。試行錯誤の例をもう一点、あげておきます。魔法陣の問題です。
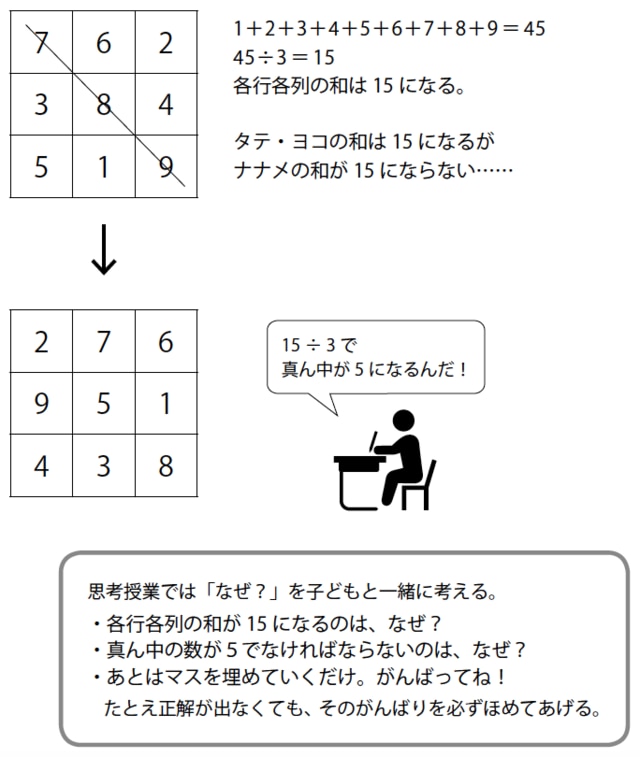
正方形型の9つのマスに、1から9までの数字を一回だけ使い、タテ・ヨコ・ナナメに並ぶ3つの数の和が同じになるように、数字を入れる問題です。
でたらめ型の試行錯誤なら、適当に数字を入れていき、それでは解決しないことがわかって諦めてしまうでしょう。これでは考えていることにもなりません。
解き方を教えるのではなく、これを使って、子どもの頭が動き続けるようにするにはどうすればよいか。ぜひ、お父さんも一緒に考えてあげてください。非常に面白い問題です。いろいろな解き方があります。
例えば、どこか端っこの数字を決めてしまえばどうなるか。こう考えて、他の数字を置いてみるのは立派に試行錯誤です([図表])。
[図表]1から9の数字をすべて使ってタテ・ヨコ・ナナメの合計が同じ数になるように並べなさい。
何らかの見通しを立てて、試行錯誤しながら考えていく。これは算数に限らず、いわゆる理系科目全般に共通する考え方です。算数を通じて考える力を身につけた子どもは、同じ理系科目の理科も自然とわかるようになります。理科で学ぶ項目、例えばテコ、滑車、バネ、浮力、電気などは、考える力をつけるための良い材料となります。
生物分野などは、それこそ「なぜ?」「どうして?」と不思議に思うことがいくらでもあるでしょう。化学や地学、天文学などの領域にも考える力を身につけた子どもにとっては、自分で考えるネタの宝庫みたいなものです。
もちろん基礎的な知識はいくつか覚える必要がありますが、それさえマスターしてしまえば、後は考えればわかる。考える力をしっかり養っておけば、小学校はもちろん、中学校、高校と進んでも、理系は得意科目となるはずです。
物事を筋道立てて考える力は、あらゆる科目に応用可能
では、算数で考える力を養えば、その力は国語にも活かされるのでしょうか。結論からいえば、間違いなく活かされます。複雑な文章題を解くカギは、まず問題の意味を理解することでした。つまり、考える力がつけば、文章を読んで理解することができるようになります。
文章を読んで理解することは、すなわち、文章として書かれている情報を整理することです。もちろん、算数の文章問題と国語の長文問題を比べれば、文字数は圧倒的に国語の長文問題の方が多くなります。つまり、国語の長文は情報量が多いのです。
けれども、いくら文章が長いといっても、全文が一つの文章で書かれているわけではありません。長い文章といっても、結局は短い文章がいくつも集まって構成されているのです。
であるならば、一文一文を読んで、書かれている内容を整理していけばよいのです。国語の場合は、年齢を重ねて一般常識などを身につけるにつれて、理解力も増していきます。算数の問題を通じて考える力を養っておけば、国語もできるようになるのです。
中学に入って習う英語も同様です。英語の場合、リスニングとスピーキングに関しては、慣れるための反復練習が必要です。けれどもリーディングとライティングについては、やはりものごとを筋道立てて考える力があれば、理解が早くなります。
なぜなら、英語は日本語よりもはるかに厳格に、ルールに従って書かれているからです。文章の構造、骨格は、一定の法則によって決められています。基本的な構成を見極めることができれば、後は単語の意味がわかるかどうかの勝負です。意味のわからない単語は辞書で調べれば済みます。
では、文系科目の象徴ともいえる社会はどうでしょうか。地理や歴史を学ぶ時に大切なのは、年号や土地の名前、人物などを覚えることだけでしょうか。
実は社会を学ぶ時のポイントも、他の科目と同じです。「なぜ?」と「どうして?」から入っていくと、理解しやすく、理解したことなら覚えるのが容易になります。
歴史上のほぼすべての出来事は、人によって起こされています。人が行動する背景には、それも何か歴史的な出来事が起こる際には、必ず理由があるはずです。それは時代的背景なのかもしれないし、誰かと対立していたからかもしれません。義憤に駆られた行為や、宗教的な理念に基づいている場合もあるでしょう。
けれども、いずれにしても、すべてに何らかの理由があるはずです。であるならば、その理由を考えることができるはずです。いつ、どこで、何が、どのように起こったのかは歴史的な事実であり、その時最も大切なのが、誰が「なぜ」そのような行動を起こしたのかです。
さすがに小学校の社会では、そこまで考えることは少し無理があるかもしれません。けれども、中学生以上になれば、歴史、地理、政治経済なども、このように考えて理解することで、それほど苦労しなくても成績を伸ばすことが必ずできるのです。



























