検索
入試対策における「基礎」とは？
首都圏の私立小学校入試は8月～10月に願書受付開始、9～11月に選考が行われるスケジュールが一般的です。
こぐま会の「セブンステップスカリキュラム」では、1年間の学習を7つのステップに分け、基礎段階→応用段階→総まとめと進みます。4月までに「基礎段階の学習」を終える予定ですが、ここまでをどれだけしっかりと身につけるかが、過去問を含めた応用段階の学習を支えるために大事です。
では、入試対策における「基礎」とはなんなのでしょうか。
易しいから基礎で、難しいから応用なのではありません。子どもたちが物事をどのように理解していくのか、また、なぜある段階になると問題が解けなくなってしまうのか。そうした子どもの実際から「基礎」はなにかを考える必要があります。
その意味で、できない問題の根拠を分析することが一番わかりやすいと思います。私たちが学習の順序を守り、それぞれの領域の課題の系統性を重んじた学習を実践しているのは、「基礎」をしっかり身につけなければならないと考えているからです。
3つの課題から解説する、基礎学習の大切さ
抽象的な話にならないよう、実際の入試問題を使って「基礎学習の大切さ」をお伝えしたいと思います。今回は3つの課題を取り上げます。
★課題①「言葉づくり」…近年頻出の言語領域の問題
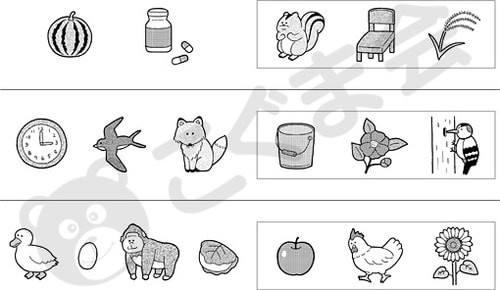
まずはじめは、最近の入試でよく出題される言語領域の「言葉づくり」という課題です。
一音一文字・言葉づくり
●左のものの名前の真ん中の音を使うとどんな言葉ができますか。それぞれ右から選んで〇をつけてください。
それぞれの言葉の指定の音を使って新しい言葉をつくるという問題です。
1番はじめの音を使って言葉をつくる場合は易しいはずですが、真ん中や下から2番目の音を使ってつくるとなると結構難しくなります。こうした入試問題の基礎は、「一音一文字」という考え方に根拠があります。日本語は、いくつかの音が組み合わさって言葉が形成されている、という考え方によるもので、たとえば「リンゴ」であれば3つの音でできていて、最初は「り」、2番目は「ん」、最後は「ご」の音がつく、という考え方です。
この一音一文字の考え方「どこになんの音がつくのか」は、ステップ1の言語領域で学習しますが、その考え方が応用されて、「しりとり」や「同頭音」や「同尾音」の学習につながり、そのあと「言葉つなぎ」や「言葉づくり」に発展していきます。
一音一文字やしりとりは、絵カードを使った学習が有効です。基礎を身につけるためには試行錯誤する時間が必要ですので、基礎段階からペーパー中心の学習ではなく、今回の場合はまず絵カードを使った練習をおこなってください。
★課題②「四方からの観察」…やや抽象的なつみ木を使った問題も頻出
では次の問題を見てみましょう。これは「四方からの観察」という課題で、一つのものの見え方が、見る場所によって変わるというものですが、最近の入試では、具体物でありながらやや抽象的なつみ木を使った四方からの観察がよく出題されています。ある学校の入試で出題された以下の問題は、私たち大人にとっても難しい問題です。
四方からの観察を含んだつみ木の数当て
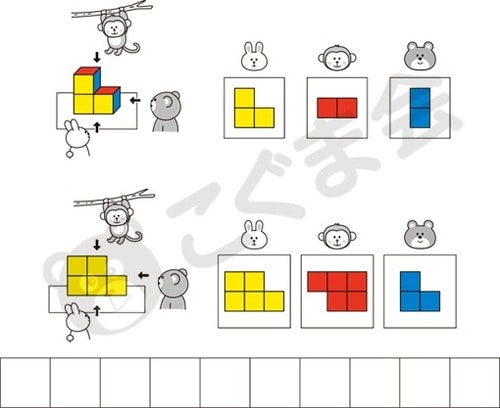
上の絵を見てください。テーブルの上のつみ木をまわりから動物が見ています。前から見ているウサギはつみ木の黄色いところ、右から見ているクマからはつみ木の青いところが見えます。木の上から見ているサルからはつみ木の赤いところが見えています。
●下の絵を見てください。下の机の上のつみ木をまわりから動物たちが見ると、それぞれ右のように見えました。机の上の形はいくつのつみ木でできていますか。その数だけ下のお部屋に青い〇をかいてください。
この問題を自分の力で解くために必要な「基礎学力」となんなのでしょうか。
1. 場所が変わると同じつみ木も違って見えるということが理解できているか
2. 左右関係の理解がどこまで身についているか
3. 立方体を表現する場合、奥行きのない表現（つまり真四角）で理解できるか
4. 3つの方向からの見え方を総合して、うしろに隠れているつみ木の存在が理解できるか
こうした基礎的なものの見方ができてこそ、この問題は解決可能になるのです。この基本練習をしないまま理解できない子どもに解き方だけを教え込み、その場でわかったつもりになっても理解してはいないのです。
同じような問題を解かせてみるとよくわかります。説明を受けてわかったつもりになっても、その考え方が他の問題を解く際に生かされていなければ「転移する学力」にはなりません。学びの系統性を理解しないまま大人が教え込んでも、一つの学びが次の学びの基礎になっていかず、無駄な学びを多くしていることになるのです。
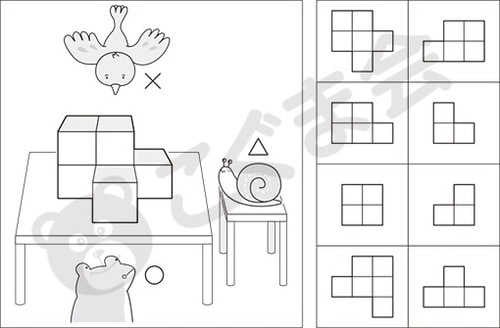
上のような複合された入試問題を解くためには、まず一つのものの見え方を、その場に行かずに描いてみたり、実際につみ木を積んでみたりといった観察をしたうえで、以下のようなペーパーを使った基本問題をたくさん練習する必要があるのです。
四方からの観察
真ん中のつみ木を生き物たちが見ています。
●カエルから見た形に〇、カタツムリから見た形に△、上を飛んでいる鳥から見た形に×を右の絵につけてください。
★課題③「交換」…将来学ぶ「かけ算」や「わり算」の考え方が基本
もう一つ入試問題を題材に考えてみましょう。以下の問題は「交換」と呼んでいる問題で、将来学ぶ「かけ算」や「わり算」の考え方が基本にある問題です。
交換
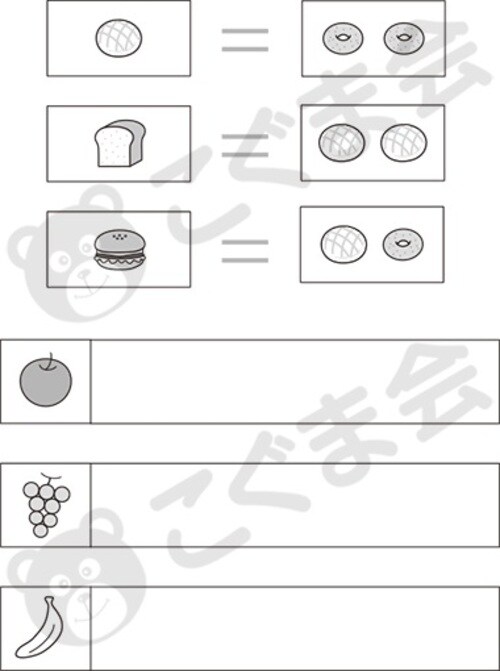
下のお部屋を見てください。メロンパン1個は、ドーナツ2個と交換してもらえます。食パン1斤は、メロンパン2個と交換してもらえます。ハンバーガー1個は、メロンパン1個とドーナツ1個と交換してもらえます。
●メロンパン4個は、食パンいくつと交換してもらえますか。その数だけリンゴのお部屋に〇をかいてください。
●食パン2斤は、ドーナツいくつと交換してもらえますか。その数だけブドウのお部屋に〇をかいてください。
●ハンバーガー4個は、食パンいくつと交換してもらえますか。その数だけバナナのお部屋に〇をかいてください。
考える力を求めるとてもいい問題だということで、授業でも扱っています。この問題を解く基礎的な学力とはなんなのでしょうか。
1. メロンパンから食パンの数を求めるには、わり算の包含除の考え方が必要です
2. 食パンからドーナツを求める問題は、かけ算の考え方に加え、置き換えの考え方も必要です
3. ハンバーガーから食パンを求める問題も、包含除だけでなく置き換えの考え方が必要です
かけ算とわり算の包含除の関係を考えれば、たとえば「メロンパン1個は、ドーナツ2個と交換できる」とした場合、「メロンパン3個は、ドーナツいくつと交換してもらえるか」と同時に「ドーナツ8個は、メロンパンいくつと交換してもらえるか」の両方の質問に答えられなくてはなりません。
この課題を子どもに与えた場合、メロンパンからドーナツはわかっても、ドーナツからメロンパンを問いかける問題になるとやや立ち止まります。
その意味で、違う視点から問いかけることが大事です。そして、この問題を難しくしている「置き換え」の課題は、実際になにかに置き換えて交換する経験をさせることが大事です。
私たちは銀行ゲームなどを通して、一度なにかに置き換えて、もう一度求めているコインに換えるという経験をさせてから、こうした問題に取り組ませています。
こぐま会では、交換の課題については、シーソーのつりあいの考え方と一対多対応の考え方をしっかり身につけることを基礎と考え、実際にシーソーを操作したり、お客さんごっこで1人に配る数をいろいろ変えて全体の数を考えさせたり、その逆に、全体の数から1人に配る数を指定して何人に配ることができるかなどを考えさせる学習を積み上げています。
自分で考え、考えのプロセスを説明できることが大切
実際に出された3つの入試問題を紹介して、「基礎学力とはなにか」をお伝えしました。
難しい過去問として取り上げられる、以上のような問題を解決するために、多くの場合、繰り返しの練習で身につけていくという方法がとられます。極端ないい方をすれば、過去問を繰り返し、徹底して訓練すれば合格できるといったとんでもない発想で対策をとる場合もあります。
これからの時代の入試問題は、自分で考え、考えのプロセスを説明できなくては対応できません。それぞれの課題を解くための基礎がなんであるかをしっかりと押さえ、それを徹底して学ぶことが、私たちが重視する「転移する学力」へとつながります。
ステップ1からステップ4までの学習は、そうした「基礎」を学ぶための学習を徹底しておこないます。そのためこの時期には、ほとんど過去問を使った授業はしません。具体物を徹底して使い、考え方の基礎をしっかり身につけていただきます。
そうしたやり方に対し、早く難しい過去問トレーニングをやってほしいという要望も出てきますし、そのようなご家庭では先取りして難しい過去問トレーニングをやり始めます。こうした学びの系統性を無視した対策では、結局合格につながりません。
そうした先走りの対策で成功した例はほとんど見たことはありません。基礎をしっかり固めることが、遠回りのようでも最後は合格につながるのです。
久野 泰可
こぐま会代表
