数値管理は日本でも重要度を増してきた
日々、新型コロナウイルスのニュースがさまざまなメディアで流れ、本日の感染者数や重症者数、陽性率などさまざまな数値情報が発信されています。新型コロナウイルスだけでなく、経済やIT業界でもこの数値管理は、日に日に重要度を増しており、「ビックデータ」「データドリブン」と言ったデータの必要性や活用を謳う言葉も耳にすることが増えてきました。
早稲田大学の文系の代表である政経学部も、入学試験に統計学を含む数学が必須になり、多方面でその必要性が目立ってきました(ちなみに、早稲田大学の政経への数学が必須になった初年度は著しく受験者数が減少したそうです)。
一方で、気づかないところで多く利用されているのが、「素数」です。SSLと呼ばれる暗号化の技術があるのですが(サイト見る時にhttpsで表現されたり、ブラウザによっては鍵のマークが表示されるもの)、この暗号化とは、とてつもない大きな素数を鍵として利用し、中身を暗号化しているものになります。

現在ではこの鍵による暗号化も公開鍵と復号鍵を別々に用意し(ドアを閉める鍵と開ける鍵が異なるイメージ)、公開鍵を暗号化するという、現在のRSA法があるのですが、それには中学で習った「素因数分解」が一方向性をもった関数として利用されています。
また、よくあるITででてきそうな短縮名称ですが、このRSAはマサチューセッツ工科大学の研究者のRivest(リベスト)、Shamir(シャミア)、Adelman(エーデルマン)の頭文字から取られていて、内容を意味するものになっていません。
このように、数学を用いて説明し、情報共有をすることが増えてきましたが、見る側も正しい知識をもって読み解かないと、大きな勘違いをしてしまうことがあります。
身近な数学利用の例を書くと、一番多いのが「平均」や「推移」でしょう。前述した新型コロナウイルスの事案もそうですが、結果や変化を表現するときには多くこの項目での数値結果が利用されます。ただ、気をつけなければいけないのが、「平均値」というマジックです。
下の図は、共に平均年収300万円の集団ですが、内容が全く異なります。単純に平均年収が上がったという結果を見るだけでなく、中身を見てどのような構成になっているのかを把握したほうが、正しい理解ができます。
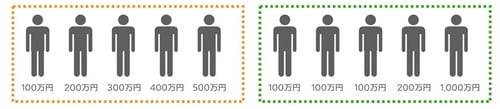
数学的には「分散」や「標準偏差」というような指標があり、ばらつきを数値化して表すことが可能です。細かい説明は割愛しますが、標準偏差が低いとばらつきが少なく、高いと多いというような指標になっています。いろんな企業からの提案書や結果の報告でも、おやと思ったときには、ばらつきがどうなっているかを質問することで、本当の結果が見えてくるようになります。






























