思考力は高いのに「数学が苦手」な人が、できていないこと

 

実際に数学を教える側の視点で見ると、点数が伸びない生徒の多くは②と③の部分で苦戦していることが分かります。

 

②でつまずく、つまり問題を正しく理解できていない場合は、正解にたどり着くことはできません。問題文には、解法につながる情報がたくさん含まれていますから、そこから「使える情報」と「最終的に求めたいもの」を正確に把握することを意識しましょう。

 

「正確に把握する」とは、ただ書かれていることの意味が分かるということではなく、出題者がその情報を与えた意図や、どの知識と結びつけてほしいと思っているかまで理解するということです。問題文には解答のヒントが隠れています。それを正しくキャッチして、必要な公式や定理を正しく想起することができれば、たいていの問題で③の「方針を決める」という部分はクリアできます。

 

具体例を見てみましょう。

 

「辺AB= 6、辺BC= 4、辺CA= 5の三角形ABCにおいて、外接円の半径Rを求めよ」

 

教科書の練習問題に載っているような単純な問題ですが、この問題文から次のことを読み取ることができます。

 

1．3辺の長さが分かっている→「3辺の長さ」＝「使える情報」なので、3辺の長さを含む式を使う

 

2．外接円の半径を求めたい→「外接円の半径」を含む式を作りたい

 

※「xの値を求めたい」→「x = ～ がゴール」→「xを含む式が必要」ということ

 

これらを読み取ることができ、必要な定理を正しく覚えていれば、次のことをイメージできます。

 

1．3辺の長さを含む式を使う→「余弦定理」をイメージ

 

2．外接円の半径を含む式を作る→「正弦定理」をイメージ

 

※余弦定理は「cosA=（b2+c2−a2）/2bc」、正弦定理は「a/sinA=2R」

 

ここから分かることは、次のとおりです。

 

1．余弦定理に3辺の長さを当てはめると、cosAが求められる

 

2． 正弦定理でRを求めるためにはaとsinAの値が必要だが、aの値はもともと分かっているのでsinAの値が求められればRは出る

 

そして、この二つを照らし合わせると次のことが分かり、結論が得られます。

 

・ cosAからsinAを求められれば答えは出る→sin2A+cos2A=1を利用すると、cosAからsinAは求められる→次の手順で解けばよい。

 

「余弦定理でcosAを求める→cosAからsinAを求める→正弦定理によりRを求める」

 

この問題はほかにもいくつか解法がありますが、少なくとも右記のことがイメージできて、かつ正確に計算処理を行うことができれば、正答できる問題です。先述の解き方が分かるために必要なことは、次のとおりです。

 

1．定理の正しい理解（「余弦定理」：3辺+ 1角という4つの情報を含む式で、そのうち3つを数字で埋められれば残り一つが分かる。「正弦定理」：1辺+ 1角+外接円の半径という3つのデータを含む式で、そのうち2つを数字で埋められれば残り1つが分かる。「sin2A+cos2A=1」：cosAかsinAのどちらかが分かっていれば他方を求められる）

 

2．問題文から使える情報（3辺の長さ）と求めたいもの（外接円の半径）を読み取り、それらを含む式を使うことが求められていると気づく

 

3．その式を使って得られる値、先の展開を考えて、解くうえで必要な情報を洗い出し、手順を決める

 

必要な知識を正しく理解していることはもちろん、②の「問題を正しく理解する力」がなければ正しい解法を導くことはできません。問題文を読むときは、使える情報を明確にして、その情報が与えられた理由や、どの公式や定理に結びつけられるものなのか、というところまで考えられるようになると、解ける問題が劇的に増えていきます。

 

また、③の「方針を決める」、つまり公式や定理を使って処理をした結果を見通すことは、複数の公式や定理を組み合わせて答えを出すために必要不可欠です。最初に余弦定理を使い、最後に正弦定理を使って答えを出すことは分かっても、それだけですべての手順が分かるわけではありません。余弦定理を使うとcosAが出るということと、正弦定理でRを出すためにはsinAの値が必要だという情報がそろうことで、初めてcosAの値を使ってsinAの値を求めれば良いことに気づくのです。

 

解法に必要な知識を選び出して、正しい手順をとるためには、公式や定理を使って求められる値と、その値を利用して得られる次の展開を見通す思考力を養う必要があります。

課題は発見して「もらう」もの

ここまで書いてきたとおり、数学の問題が解けないときに考えられる課題はいくつかに分割できます。

 

一方で、課題を自分ひとりで見つけることは簡単なことではありません。例えば、ある公式を覚えていないために解法が思いつかない、という課題があるとします。その場合、その公式を覚えていないという状態は、つまり、その公式が頭の中にないということ。「あるべきものがない」ということに気づくためには、そもそも「それが存在する」ということを知っておかなければならないのですから、気づくことは原理的に不可能でしょう。

 

ですから、課題を特定してその対策を行う場合、必要な知識やスキルを網羅的に持っている講師などに見てもらうほうが、はるかに効果的なのです。

 

参考書などを片手に、知識の欠落に気がつく可能性はゼロではありませんが、受験にはタイムリミットがあるということを忘れないでください。十分に知識のある人なら、足りないものをすぐに特定してくれます。自分でやろうというモチベーションは、課題の特定ではなく、克服するための訓練に向けてください。できる人に聞いて課題を発見してもらい、対策を立てることが近道です。

思考の可視化トレーニング

人に見てもらい、課題を発見してもらうためには、自分が問題を解いたときに考えたことをすべてノートに記載しておくと効果的です。問題を解くときの頭の中をすべて可視化するのです。

 

例えばノートの見開きの右ページに考えたことをすべて書いていき、「この方針でいけば正解できる」と分かれば左ページに解き始めるといった方法です。

 

このとき、方針が明確に分からない場合は、左ページには何も書かなくても良いのです。

 

解答の方針が分からない場合は、試したことや考えたことに問題があるということですので、知識のある人が右ページを見れば簡単に課題を発見することができます。

 

解き方も分かっていないのにやみくもに解いていくことは、仮に正解したとしてもそれは偶然であり、再現性の低いものです。

 

ノートに思考のプロセスを残すというこの方法では、不正解の場合はもちろん、正解している場合でも課題を発見できます。解答だけ見ると正しい場合でも、考え方には解決すべき課題が含まれていることがあります。

 

解き方を選択する根拠が正しくなければ、その解き方をいろいろな場面で使いこなすことはできません。解答ページに書かれてあることは、結果でしかないので、根拠を確認することはできません。しかし検証ページがあれば、根拠をチェックすることもできるし、試したことや思ったことのうちおかしな部分を修正することもできるのです。

 

［図表1］解けなかった場合のノートの例

講師がチェックして、足りない知識を補っている。

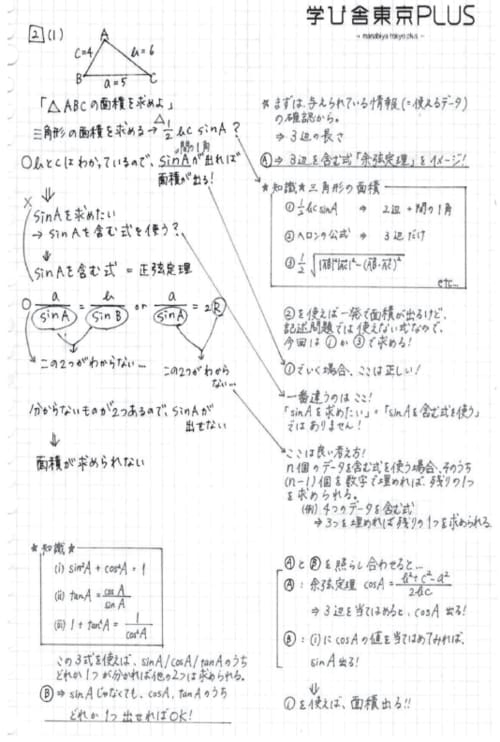
［図表2］正解した場合のノートの例

解き方は正しいが考え方に誤りを含んでいるため、講師が修正している。