年金受給額の「世代間格差は6000万円」…1965年生まれが損得の“境”

年金制度には大きな世代間格差が存在する。「親が年金をもらえば、子供は親の老後の面倒を見る必要がないから、子供も年金制度から利益を得ている」という主張も存在するが、果たしてそれは正当だろうか。前日銀副総裁・岩田規久男氏が解説する。　※本連載は、書籍『「日本型格差社会」からの脱却』（光文社）より一部を抜粋・再編集したものです。

※写真はイメージです／PIXTA

「お金」の最新情報をチェック！メルマガ登録はこちらから

年金の「世代間格差」は「6000万円」にもおよぶ

日本の格差問題を考える場合、現在の所得格差や富の格差だけでなく、年金に関する「世代間格差」問題にも目を向ける必要がある。

これは、世代間で生涯に受け取れる年金給付総額と生涯支払った年金保険料総額との差が大きく異なるという問題である。

この差を考えるときには、年金保険料を支払った時期と年金を受け取る時期が異なる点を考慮する必要がある。その場合、合理的に考えると、支払った年金保険料総額と比較されるべき年金給付総額の価値は、適切な割引率で割り引いた現在価値である。

例えば、最も分かりやすい単純なケースを想定して説明すると、次のようになる。

【ケース1】

現在、年金保険料を50万円支払って、1年後に、55万円の年金給付を受けるとしよう。それに対して現在、50万円を預金すると、1％の金利が得られるとしよう。

1年後の預金の元利合計は50.5万円になる。これは、1年後の50.5万円が、現在の価値にすると50万円（つまり現在の預金額）に相当することを意味する。この50万円は、1年後の50.5万円を（1＋金利÷100）で割った値に等しい。

そこで、この金利（ここでの例では1％）のことを、1年後に受け取る金額を現在価値に換算するときの割引率という。この1％の割引率を使うと、1年後の年金給付額55万円の現在価値は約54.5万円になる。

したがって、年金給付額の現在価値と年金保険料額との差は4.5万円になる。このケースでは、4.5万円が年金制度から受け取れる利益になる。この利益を年金の純受給額といい、年金給付額の現在価値54.5万円を支払った年金保険料額（50万円）で割った値を年金の給付負担倍率という。この例では、給付負担倍率は1.09である。

【ケース2】

ケース1に対して、1年後の年金給付額が45万円であるとしよう。この現在価値は、割引率をケース1と同じ1％とすると、44.55万円になるから、年金給付額の現在価値と年金保険料額との差はマイナス5.45万円（マイナスの年金純受給額）になり、損失が発生する。年金給付負担倍率は0.89になり、1を割る。

ケース1では、年金給付負担倍率は1を上回り、年金加入は得になるが、ケース2では、年金給付負担倍率は1を下回り、年金加入は損になる。

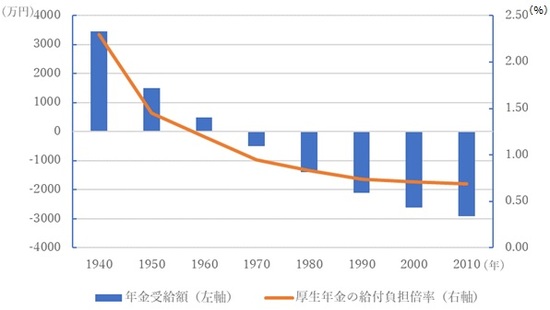
鈴木亘（2012）は最近の金融市場を考慮した割引率と平均的な年金給付期間を設定し、［図表］のような、生まれ年度ごとの厚生年金給付負担倍率と年金純受給額を試算している。