補償額が大きな契約は、一部を再保険に出して額を抑制

前回の続きです。

よりイメージを持ちやすくするために、図を使って説明しよう。

［図表］再保険のイメージ

出再：他社へ再保険に出すこと　受再：他社から再保険を引き受けること

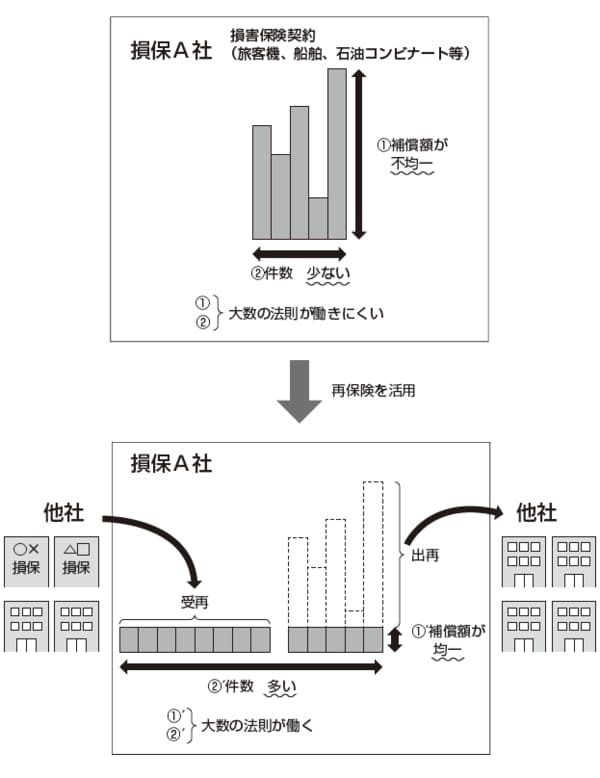
大数の法則を成立させるためには、契約の件数が多くて、それぞれの補償額が同程度なのが理想である。それでは、現実の損害保険契約がどうなっているかというと、図の上のグラフのようになっている。契約件数が少なく、補償額も不均一ということだ。

ここで再保険を用いると、大数の法則が働きやすい理想の状態に近づけることができる。そのことについて示しているのが、下のグラフである。自社で保有している契約のうち補償額が大きなものについては、一部を再保険に出すことで補償額を抑制する。そうやって契約毎の補償額を均一に近づけて、「同一性」を担保するわけだ。

また、大数の法則を働かせるためには契約件数を増やす必要がある。そのためには、他社から多数の再保険契約を引き受ければよい。自社だけでは契約件数を十分に確保できないので、他社から再保険契約を引き受けることで、大数の法則が働くレベルまで保有契約件数（自社の契約件数＋他社から引き受けた再保険契約件数）を増やすことができるわけだ。

船舶保険のような規模の大きな損害保険契約は、このように再保険を通じて大数の法則を働かせている。

自動車保険は「事故発生率」を使って理論を組み立てる

また、自動車保険のような小粒の契約についても、大数の法則が活躍している。生命保険では死亡率を使って理論を組み立てていたが、自動車保険の場合は事故発生率を使って理論を組み立てる。

さらに、生命保険と違って定額保障ではないので、事故が発生した場合にどれくらいの損害額になるかについても理論を作らないといけない。これについては、膨大な実績データの研究や理論的な考察により、事故の損害額がどういう分布に従うかが分かっている（具体的にいうと、損害額の少ない事故は起こりやすく、損害額の大きな事故はあまり起こらないので、損害額を横軸、発生件数を縦軸にとると、左側に偏った分布になる）。

そして、事故が発生する確率についての理論と、事故が発生した場合の損害額についての理論を組み合わせることで、損害保険の理論が作られるのだ。その後は生命保険と同様に、大数の法則を働かせるために「独立性」と「同一性」を担保すればよい。自動車事故は基本的にお互い無関係に起こるので「独立性」は担保される。そして「同一性」についてだが、自動車の価格は大部分が1千万円以下で、高級車の代表格であるランボルギーニでも4千万円くらいなので、数十億円の損害額なんてことはありえない。ちなみに、アンティーク車の中には価格が数十億円というものもあるらしいが、そういうのはコレクション用であって、乗り回して遊ぶ人はいないだろう。従って、特別な人がいないので、「同一性」も保たれているといえる。

その結果、大数の法則によって理論と実際が一致するので、補償が可能になるのだ。また、高級車については保険会社による加入審査が実施され、居住地域の治安や自然災害のリスク（大雨による浸水など）、車庫のセキュリティ等が調査されることがある。そして、場合によっては加入を断られる可能性もある。これは、「同一性」を保とうとする努力の一環といえるだろう。