リターンとリスクについて
投資の世界におけるリターンとリスクは、普段私たちが使っている意味とは少し異なり、「平均値」と「標準偏差」で示されます。今回は平均値や標準偏差をご説明しながら、投資の世界におけるリターンとリスクについてご説明したいと思います。
平均値とは?
まず、平均値について考えていきたいと思います。平均値の計算方法は皆様ご存知の通りで、それぞれのデータを足し合わせ、その合計をデータ数で割ることで算出できます。
ところで、平均値という考え方は非常に便利ですが万能ではありません。平均値をそのまま鵜呑みにしてしまうと、大きな誤解をしてしまう可能性があります。平均値が全体のデータを網羅的に表している数値ではない可能性があるからです。
その事をテストの点数の例で考えてみたいと思います。
まず、A君80点、B君65点、C君60点、D君75点の例1のケースです。例1の平均値は70点です。この70点という平均値は、4人それぞれの点数からそれ程かけ離れた点数ではなく、ある程度全体像を表しているように見えます(図表1)。次にA君5点、B君100点、C君25点、D君50点の例2のケースです。このケースですと、4人の平均値は45点となります。D君以外の点数は平均値から離れており、このクラスはだいたいみんな45点ぐらいだなと考えてしまうと大きな誤解をしてしまいます(図表2)。
[図表1]例1におけるそれぞれの点数と平均値
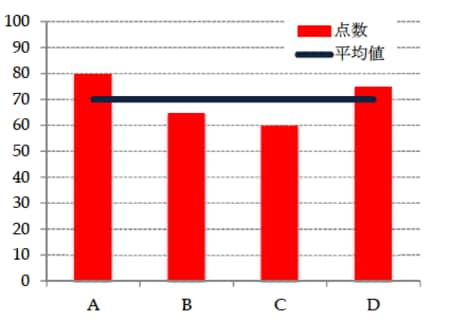
[図表2]例2におけるそれぞれの点数と平均値
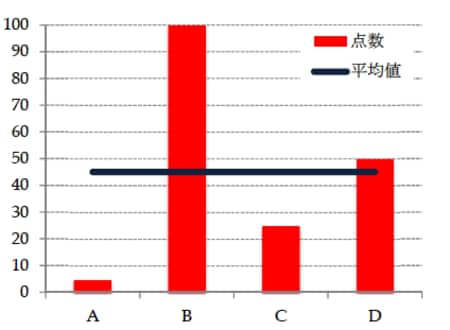
例1と例2の違いはどこにあるのでしょうか。それはそれぞれの点数のバラつきにあります。例1はそれぞれの点数にそれ程大きな差は見られませんが、例2では各人の点数に大きなバラつきがあります。
このように、バラつきが大きいデータ群から平均値を算出してもデータ群の全体像を正しく把握する事はできません。つまり、平均値で全体を把握できる場合と把握できない場合があるのです。では平均値に対してそれぞれのデータがどのくらいバラついているのかをどうやって把握すれば良いのでしょうか。その答えが、「標準偏差」です。
リスクを数値化する「標準偏差」(1)
標準偏差は「バラつきの大きさ」を表す数字で、リスクの大きさを数値化するものです。「極端なケースを除き、だいたいこのくらいの範囲の中に収まる」という範囲を教えてくれます。まずは、標準偏差を理解する為に必要な、「偏差」と「分散」からご説明します。
図表3の「平均値」の隣に、「最大」と「最小」を載せています。これはそれぞれのテストの最高点と最低点を表示したもので当たり前ですが、例1と例2の全員のテストの点数は、この「最大」と「最小」の間に収まります。例1の最高点は80点で最低点は60点ですから、例1のテスト結果は最大80点から最小60点の範囲に全て収まります。例2の最高点は100点で最低点は5点と、良い点数と悪い点数の差が大きくなっていますが、全ての点数はこの間に収まります。ここで、例1と例2のテストの「平均」がそれぞれの点数からどれくらい離れているか考えてみましょう。例1の平均は70点であり、それぞれの点数に近いように思えます。一方、例2の平均は45点であり、それぞれの点数からかけ離れているように見えます。このことを調べるには、「偏差」を計算してみるとよく分かります。
[図表3]例1・例2の平均値、最大・最小
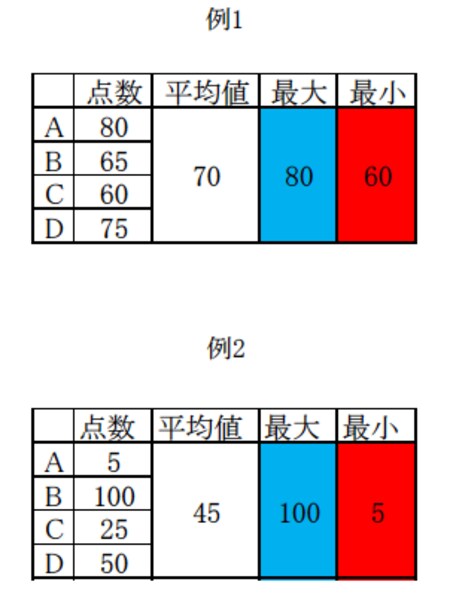
「偏差」とは、それぞれのデータが平均値に対してどれだけ離れているかを数値で表したものです。こう言うと難しく感じるのですが、各データの値から平均値を引くだけの簡単な計算で求められます。偏差を計算してみると、例1よりも例2の方が偏差の数字が大きい事がわかります(図表4)。これは、例2の方がデータのバラつきが大きい事を意味しています。
[図表4]例1・例2の偏差、分散、標準偏差
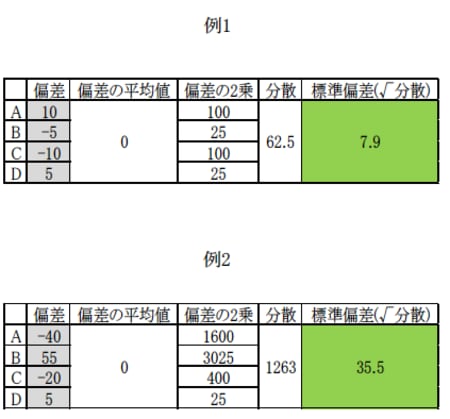
次にそれぞれの偏差の平均値をとってみましょう。偏差の平均値は0になります。プラスの偏差とマイナスの偏差が打ち消しあってしまうのです。
それでは、どのように偏差の平均値を取れば良いでしょうか。それは各偏差の値を2乗し、全ての偏差をプラスに揃えてしまえば解決します。各偏差を2乗して計算した数値の平均値を「分散」と言います。分散は偏差を2乗して求めた値ですので、そのままでは平均値との比較に使いにくいです。そこで、分散の平方根(ルート)を計算し2乗を外す必要があります。分散の正の平方根が「標準偏差」です(図表4)。分散も標準偏差も数値が大きいほどバラつきが大きいことを示します。
リスクを数値化する「標準偏差」(2)
ところで、標準偏差は「極端なケースを除き、だいたいこのくらいの範囲の中に収まる」という範囲を教えてくれますが、この「だいたい」とはどのくらいを指すのでしょうか。
これは統計学における正規分布という考え方で「平均値を中心に±1標準偏差の範囲に、データの68.26%(約3分の2)が入る」ということからきています。つまり「だいたい」とは約3分の2ということであり、「極端なケースを除き、だいたい(3分の2が)このくらいの範囲の中に収まる」と覚えておいてください(図表5)。
[図表5]正規分布図
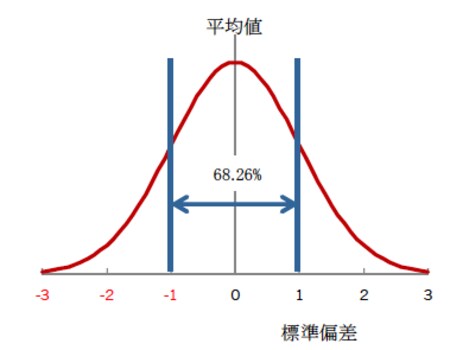
ここまで見てきたことから、平均値と標準偏差の値が分かれば、データがどのくらいの範囲にどのような割合で散らばっているかがある程度明らかになります。標準偏差が小さいということは全体のバラつきが小さいこと、平均値の周りにデータが集まっていること、また、逆に標準偏差が大きいということは、平均値から遠く離れているデータが多くあることを意味します。例1は平均70点に標準偏差一つ分を足した77.9点から標準偏差一つ分を引いた62.1点の範囲の中に、例2は平均45点から標準偏差一つ分を足した80.5点から標準偏差一つ分を引いた9.5点の範囲の中に全データの3分の2が収まるということになります。
値動きの特性を表すリスク・リターン特性
ここまでの内容を踏まえて、資産の値動きの特性を表すリスク・リターン特性のグラフを見てみましょう。このグラフは横軸がリスクを示し、右にいくほどリスクが高く、左にいくほどリスクが低いことを示します。横軸は各資産の収益率の標準偏差(リスク)、一方縦軸は各資産の収益率の平均値(リターン)を示しています。
例として日本国債を見てみましょう。リスク年率2.0%、リターン年率1.8%が示すことは、収益率の平均値が年率1.8%で、これにリスク(標準偏差)一つ分を足した年率3.8%とリスク一つ分を引いた年率-0.2%の範囲内にだいたいが収まるということになります。日本国債の平均収益率は他の資産に比べて低いですが、青い上下矢印で示した範囲内にだいたいのデータが収まり、リターンのバラつきも少なく、良いときと悪いときの差が小さいことが分かります。一方、日本株式は平均収益率は日本国債よりも高いですが、良いときと悪いときの差が激しく、日本国債のリターンを大きく下回るようなケースもあることが分かります(図表6)。
[図表6]リスク・リターン特性の例(2003年7月末~2015年7月末)
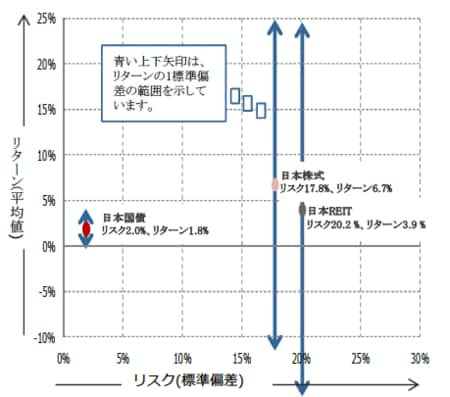
※期間中の各月のリターンを年率換算して計算し、平均値をリターン、標準偏差をリスクとして表示。
出所:ブルームバーグのデータを使用しピクテ投信投資顧問作成
このリスクとリターンの概念を理解すると、それぞれの資産が平均収益率を中心にだいたいの値動きの範囲が把握できるようになります。しかし注意しないといけない点があります。それは平均値も標準偏差も「過去」のデータから算出した値にすぎないということです。例えば米国債利回りは過去約30年間低下し、現在最低の水準にあります。今後米国債利回りが上昇を始めるとすれば、過去30年間とは全く異なった動きが展開される可能性があり、これまでの動きが参考にならないことが想定されます。過去の動きが必ずしも未来の予想にはなり得ないことは心に留めるべきでしょう。
当レポートの閲覧に当たっては【ご注意】をご参照ください(見当たらない場合は関連記事『実践的基礎知識 リスク編(3)<リターンとリスクについて> 』を参照)。





























