フェアに比較すると見える“不都合な真実”
ということで、ここからは他ではなかなか見かけないアプローチで、積立投資を真面目に、そしてフェアに検証してみましょう。この連載は『GeekなNISA』ですからね。
今回は「モンテカルロ・シミュレーション」という手法を用いて、積立投資と一括投資の比較実験を行います。名前は仰々しいですが、要するに「大量の乱数を使ってシナリオをシミュレーションし、どちらの手法が確率的に優れているかを検証するもの」と考えてください。
シミュレーションの前提として、投資の収益率は短期的には正規分布に従ってランダムに変動するものと仮定します※。
※ 統計学において一般的な前提の置き方です。
もちろん、現実のマーケットで価格変動が完全に正規分布に従う保証はありません。しかし、インデックス投資の理論的基盤となっているEMH(効率的市場仮説)※1やCAPM(資本資産価格モデル)※2の枠組みでは、これは妥当な前提とされています。
※1、※2 EMHやCAPMについては、前々回の記事をご参照ください。
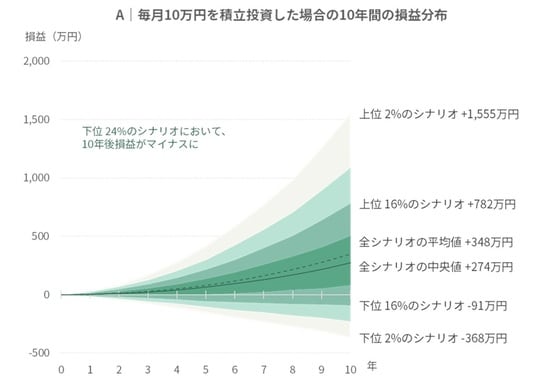
まずは積立投資について。こちらは「毎月10万円を10年間、継続して投資する」というシンプルな条件で検証します。総投資額は1,200万円です。
対する一括投資ですが、ここで重要なのはフェアな比較にすることです。先に述べたように、投資の比較は同じリスク量――つまり、「投資元本×投資時間」が等しくなるようにしなければなりません。たとえば、ワインとビールの酔いやすさを比べるなら、同じアルコール摂取量で比較すべきなのと同じです。
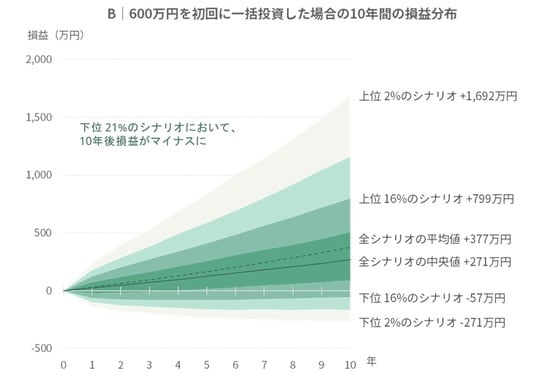
積立投資では、10年間で毎月10万円を投じるわけですから、平均して市場に投じられている資金は600万円。したがって、一括投資とのフェアな比較のためには、はじめに600万円をまとめて投資するのが適切です。これにより、両者の総リスク量が揃います。
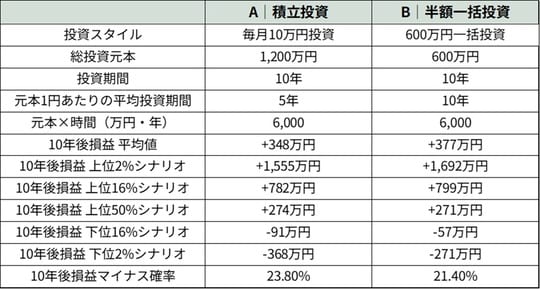
ここで、積立投資を「A」、一括投資(600万円)を「B」と呼びましょう。ただしBは、通常の一括投資(1,200万円)と混同されないよう、「半額一括投資」と名づけることにします。AもBもどちらも「期待リターンは年率5%、リスクは年率15%」の前提のもとでシミュレーションします。
もし積立投資になんらかの優位性があるのであれば、A(積立投資)の結果はB(半額一括投資)よりもいいはずです。では、実際のシミュレーション結果はどうなるでしょうか?
なんと、シミュレーションの結果は驚くべきものでした。ほとんどのシナリオにおいて、A(積立投資)よりもB(半額一括投資)のほうが優れる、という結果になったのです。
巷でよく耳にする「積立投資はリスクを抑える効果がある」といった言説は、この結果を見る限り、少なくとも本実験の前提条件のもとでは認められませんでした。