数学の応用力とは?
まずは、数学の応用問題を解くということがどういうことなのか整理してみましょう。応用問題に取り組む際にはおおむね次のような過程で考えをめぐらせていきます。

特に問題が解ける・解けないを決めるのが、②の「解答の手順の組み立て」です。応用問題が解けるようになるということは、この解答の手順を自分自身で組み立てられるようになるということです。
ただし、たとえ難解な入試問題であったとしても、未知の方法論を見つけ出して解くことを要求されることは絶対にありません。あくまで数学の基礎力を身につける勉強方法のパートで述べた典型的な解法をいくつか思い出し、それらをどういった順番で使っていくのかを考えることで正解へとたどり着くことができます。
つまり、数学の応用力とは、典型的な解法を組み合わせて考える力なのです。
典型的な解法を組み合わせて考える力
Step 1 解答の手順を組み立てる
では、解答の手順を組み立てる方法について詳しく見ていきましょう。組み立て方には大きく「順番型」と「逆算型」の2つがあります。問題に与えられた数値や条件を基に、できることを順番に行っていくのが順番型の発想です。それに対して、問題で求められているものから逆に必要なものをたどっていくのが逆算型です。
次の例題を用いて、具体的にそれぞれ順番型・逆算型の発想を確認していきましょう。
α+β、αβを2つの解とする2次方程式
x²+px+q=0の係数p、qを求めよ。
■順番型
こちらは中学校でも習った2次方程式の解法や、方程式の解が元の方程式に代入できることを用いて、できることを順番にやっていきます。
(1)x²-5x+6=0を解いて2つの解x=2,3を見つける。
これがα、βとなる。
↓
(2)x²+px+q=0の2つの解がα+β=2+3=5、
αβ=2×3=6となる。
↓
(3)x²+px+q=(x-5)(x-6)とおけるので、
右辺を展開してx²+px+q=x²-11x+30
よって、p=-11、q=30。
■逆算型
一方、こちらは数学Ⅱで学ぶ「解と係数の関係」を利用して、求めたいp、qがどのような値になるのかという視点から、逆算して必要なものを求めていきます。
(1)x²+px+q=0の解と係数の関係よりp=-(α+β+αβ)、
q=(α+β)・αβとなることを見つける。
↓
(2)α+β、αβがそれぞれx²-5x+6=0の解と係数の関係より
α+β=5、αβ=6であることを見つける。
↓
(3)これを用いて、p=-(5+6)=-11、q=5・6=30を求める。
順番型、逆算型のどちらが優れているということはありません。ただ、順番型の発想だけではなく逆算型の発想を身につけることによって、解くことのできる問題の幅は大きく広がります。ぜひとも自分のものにしてください。
Step 2 アプローチの仕方を知る
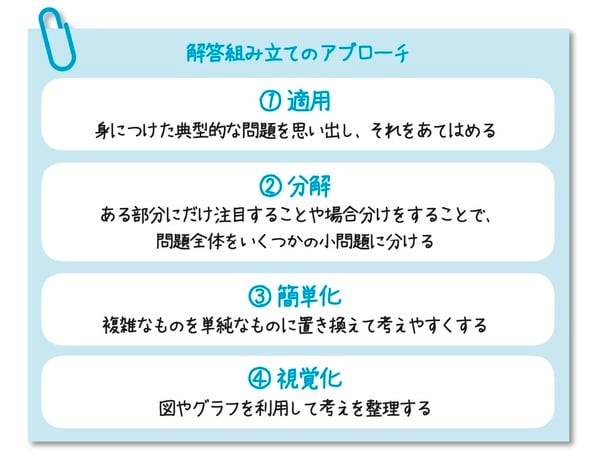
次に、解答を組み立てていくうえでポイントとなる考え方です。大別すると次の4つのアプローチが挙げられます。
これも次の例題を用いて具体的に見ていきましょう。数学Ⅱの三角関数の応用問題です。
方程式cos²θ+sinθ=aの解の個数を求めよ。
詳しい解答は省略しますが、おおよその解法の流れは次のようになります。
(1)2つの関数{y=cos²θ+sinθ…①、y=a…②のグラフの交点の個数を考える。
↓
(2)公式sin²θ+cos²θ=1を用いて、①の式をy=1-sin²θ+sinθと整理する。
さらに、t=sinθとおいてy=-t²+t+1…①'と整理する。
↓
(3)①'のグラフを書いて、aの値によって変化するy=aとの交点の個数を確認する。
↓
(4)ただし条件0≦θ≦7/6πより、
①'のグラフの-1/2≦t≦1の範囲だけに着目することを認識する。
↓
(5)1つの交点に対して、対応するθの値が複数あることを考慮する。
まず(1)の部分で、数学Ⅰの2次関数の単元でも学んだ典型的な解法「方程式f(x)=aの解はy=f(x)とy=aの交点を考える」を使っています。問題を見て似たような解法を思い出す「①適用」をしているわけです。
次に(2)でsinθとcosθの入り混じった式をsinθのみに揃え、さらには文字の置き換えによって式をシンプルな形へと変化させています。これが「③簡単化」です。
さらに(3)では具体的に関数をグラフとして表現し、視覚的に交点の個数を数えていきます。これが「④視覚化」です。
ここまでは、問題で与えられた三角関数を2次関数の問題と捉えて解いてきました。それとは別に、(4)では考えるべき2次関数の定義域(tの範囲)を、また(5)ではtの値に対応するθの値を考えています。これらは(3)までの2次関数的な思考とは切り離して、“単位円”などを用いて三角関数的な思考をして求めるものを見つけていきます。このように、問題を典型的な解法が使えるいくつかの部分に分けて考えていくのが「②分解」です。
応用問題に取り組み始めて直後は、どうしても解き方そのものに目が行ってしまい、解答全体を覚えようという意識がはたらきがちです。しかし、本当に重要なのは、ここまで説明してきたような解答の手順の組み立て方であり、それを思いつくまでのアプローチの仕方なのです。これらを身につけるために、問題を解き終えたあとに上の例で示したように、与えられた数値や条件から解答に至るまでの流れを振り返る時間をとるようにしてください。このような学習を、まずは標準レベルの問題からスタートし、少しずつ複雑な問題へとレベルを上げていきながら進めていきましょう。
とは言え、数学が苦手な人にとっては、一人で取り組むのはなかなか難しいところがあると思います。メディカルラボが完全1対1のマンツーマンで指導を行っている大きな理由の一つが、こういった問題に対する「考え方」を一人ひとりの思考過程に合わせて指導できることにあります。学校をはじめとした集団授業や少人数授業の場合、あらかじめ教える側が考えた流れを一方的に示すだけで、聞いている側からすると、どういう発想をするとこういう流れに気づけるのかはなかなか見えてきません。どういう手順で解いていくのかはわかりますが、一番知りたいはずの発想の「手がかり」や根拠は見えてこないのです。この問題が解消しないかぎり、数学に対する苦手意識もまた解消できません。
本来は、発想の「手がかり」や根拠を自分自身で見つけ出せるようになることが重要です。これができるようになるためには、問題が解けなかった、または間違えたときに、「自分はこう考えたが、どこが間違っているのか」、「このように考えてきたが、ここで止まってしまった。何を思いつかなければいけなかったのか」などの疑問を先生にぶつけながら、自分ができなかった部分を丁寧に補っていくことが重要なのです。
数学を苦手としている受験生こそ、単純に「できない」で片づけずに、正しい解答と自分の解答との違いを把握し、「解けるようになるためにはどのような知識、どのような発想が不足しているのか」を臆せず先生に質問して教えてもらいましょう。その繰り返しが、「こういう発想をすれば問題が解ける」という思考力を身につけることにつながります。
Step 3 過去問演習に取り組む
応用力を身につけるための学習に入ったら、定期的に受験大学の過去問も解いて、その大学の入試に必要な応用力を身につけていきます。ただし、ただ問題を解くだけでは過去問演習の本当の効果は得られません。過去問に取り組む目的の一つに、大学ごとの出題傾向、具体的には問題の難度、問題の分量、頻出分野、出題形式を把握することにあります。
例えば国公立大医学部では証明問題を出題する大学が多いので、証明問題に対するアプローチの練習は必須です。また、中には1つの大問に対して、解法手順のヒントになるような(1)、(2)といった小問をあえて設定しないような問題を出してくる大学もあります。こういった問題に対しては、より深い思考までできるようにトレーニングを積んでおく必要があります。
このように自分が受験する大学の出題傾向を把握するためにも、必ず受験校の過去問は解いてください。また、過去問に取り組む中でわからないところがあれば、もう一度基本に立ち返ってやり直すということを繰り返してください。この積み重ねが合格点を取るために必ず役立ちます。
さらにもう一つ、過去問演習に取り組むうえで重要なことが、本番と同様に時間を計って問題に取り組むことです。私立大医学部に見られるマークシート式の出題をする大学をはじめとして多くの大学で、かなりの処理速度を求められることになります。実際の制限時間の中で過去問に取り組み、必要なスピード感を確認しましょう。
ただし、基礎力を身につけるところでもお伝えしましたが、「スピードを上げるために途中式や図、表、筆算などを省略して時間を縮めよう」という発想は決してしてはいけません。スピードが求められているからこそ、なるべくロスを減らすよう丁寧に解いていく必要があります。むしろ、縮めるべきなのは問題を見てからその解法が思い浮かぶまでの時間です。普段から解法の組み立て方を考えるトレーニングをしっかりとしていけば、必ずそこにかかる時間は短くなっていきます。
加えて、全体の問題量・出題内容をざっと把握したうえで、どの問題から優先的に取り組んでいくのか、どの部分に時間をかけるのかといった戦略も考えてください。医学部入試は決して満点を目指す必要はありません。多くの大学では個別試験において6~7割程度の得点が取れれば合格点に達します。つまり、「どの部分で得点を取り、どの部分はあえて捨てるのか」といった取捨選択が重要になってくるのです。このような試験本番で合格点を勝ち取るための戦略を立てる力も重要です。入試までに必ず養ってください。

可児 良友
医系専門予備校メディカルラボ 本部教務統括





