仮説を立て、検証する「算数問題」は教育に最適

前回、図形に補助線を引いて試行錯誤することが、考える力を養うと記しました。試行錯誤は、ものごとを考える時に、誰もが普通に行っていることです。試行錯誤すること、すなわち考えることといってもおかしくはありません。

ただし、一つ注意が必要です。例えば図形に補助線を引くケースを考えてみましょう。この時、何も考えずただ闇雲に線を引くだけでは、試行錯誤しているとはいえません。考えていないのだから、その行為には意味はない。

一方で「この頂点と、もう一つの頂点を結べば、ここに三角形ができる」といった見通しを立てた上で、線を引くことは試行錯誤といえます。

自分なりの仮説を立てて、実行してみて、検証する。といえばビジネスの世界では、いわゆるＰＤＣＡ（プランを立てて、実際にやってみて、結果を検証して、問題点を修正した上で行動する）サイクルと呼ばれる基本です。これが試行錯誤です。

何らかの見通しを持った上で試行錯誤することが大事

例えば、次のような問題を子どもたちは、どう考えるでしょうか。

1＋2＋3＋4＋5＋6＋7＋8＋9＝？

もちろん、これぐらいなら順番に足していっても、それほど面倒な計算にはなりません。けれども、単純に足していく以外にも計算のやり方はないかな、と子どもたちに問いを投げかければ、子どもたちの頭は動き始めます。

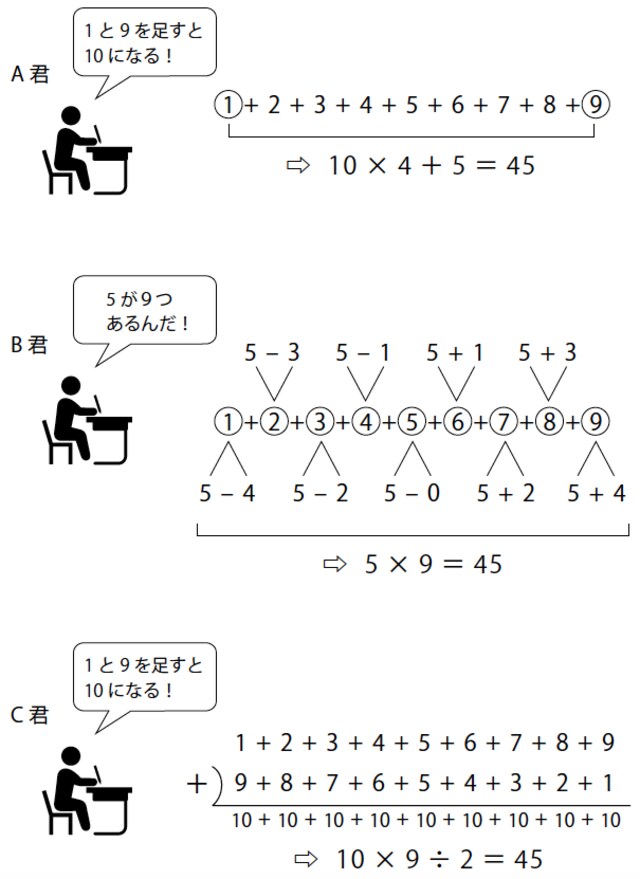
数式を見て（1・9）（2・8）・・・と足して10になるセットを見つける子どもがいます。あるいは1を5－4、9を5＋4、2を5－3、8を5＋3と考えて、結局5が9つあると考える子どももいるかもしれません。

もしかすると数学の天才ガウスが少年時代に考えたように、

1+2+3+4+5+6+7+8+9

＋）9+8+7+6+5+4+3+2+1

と考えて、10×9÷2＝45と答えを出すこともあり得るでしょう。（下記の図表参照）

［図表］1＋2＋3＋4＋5＋6＋7＋8＋9＝？

いずれの場合も大切なことは、何らかの見通しを持った上で、試行錯誤することであり、これが考えることなのです。

この話は次回に続きます。